Прямая равных издержек (изокоста)

Используя факторы производства в той или иной пропорции, Фирма стремится в соответствии с производственной функцией выпустить максимальный объем продукции. Но всегда существуют ограничения: количество денег, которыми располагает фир­ма для покупки необходимых факторов производства; цены фак­торов производства P_L и Р_к, которые задаются рынком, цена про­изводимого продукта Р.

Пусть С — общие затраты производителя; х и у — затраты факторов производства L — труда, а К — капитала. P_L и Р_К — соответственно, их цены. Тогда С = xP_L + yP_K или

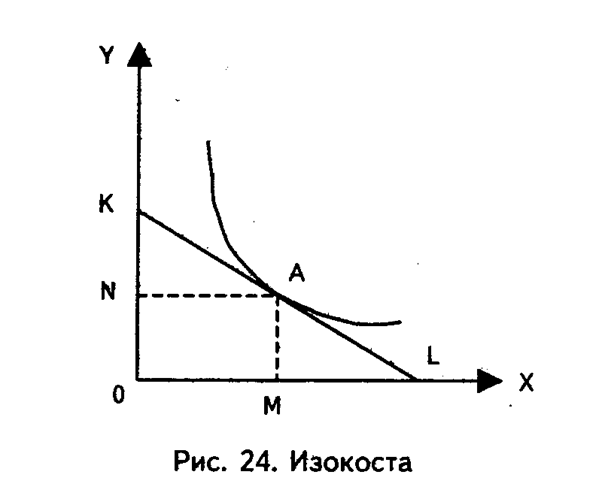
есть уравнение прямой, бесконечное число точек которой представляет комбинации факторов, использование которых ве­дет к одинаковым общим затратам. Это изокоста — прямая рав­ных издержек (рис. 24), для которой выполняется условие:

Изокоста имеет угловой коэффициент р. Это значит, что фирма может уменьшить затраты фактора L на (-P_L) и увели­чить затраты К на Р_к, и при этом валовые издержки фирмы останутся без изменения.

Точка касания А изокосты и изокванты определяет комбинацию ОМ фактора L и ON фактора К, минимизирующую издержки. В этой точке изокоста и изокванта имеют одинаковый наклон.

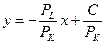
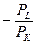Так как предельная норма технологического замещения факторов равна угловомукоэффициенту изокосты , взятому с обратным знаком, и равна соотношению предельных продуктов труда f'_L = MP_L и капитала f'_K = МР_К, то из 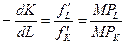и 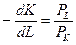следует или в другой форме 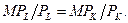Последнее равенство представляет со­бой правило наименьших издержек, используя которое можно обеспечить сочетание ресурсов для производства любого объема производства с наименьшими издержками.