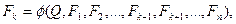Производственная функция. Свойства производственной функции

Для организации любого производственного процесса необхо­димы факторы производства.

Будем считать, что выпуск продукции Q произведен при ис­пользовании только двух факторов производства — труда L и ка­питала К. В общем виде производственная функция (1) имеет вид:

Q = f(L, К)

где f — форма производственной функции.

Производственная функция описывает технологическую вза­имосвязь между объемом выпускаемой продукции и произведен­ными затратами — затратами факторов производства, а также зависимость между затратами. В функции находит отражение максимальный объем продукции, который достигается при каж­дой комбинации факторов, то есть в определении производствен­ной функции максимизация продукции решена технически. Если в качестве независимых переменных выступают величины зат­рат, то производственную функцию называют функцией выпус­ка, если же фиксирована величина выпуска, то производствен­ная функция является функцией затрат.

При любой комбинации факторов можно достичь нескольких объемов выпуска в зависимости от эффективности организации производства. Если технология становится более прогрессивной, то фирма может увеличивать объем производства при фиксиро­ванном наборе производственных факторов. Производственная функция предполагает, что фирма использует каждое сочетание факторов с максимальной эффективностью. Если используются п факторов производства, то производственная функция в общей форме имеет вид:

Q = f{F₁ F₂,..., F_n),

где F₁, F₂,..., F_n — использованные факторы производства.

Если фиксирована величина выпуска, то производственная функция является функцией затрат и тогда затраты любого фак­тора F_h можно выразить как функцию всех остальных затрат:

где ф — форма функции.

Для укрупненного анализа и прогнозирования используется производственная функция Кобба-Дугласа ( Впервые производственная функция была построена в 1928 году для обрабатывающей промышленности США за период 1899—1922 годы и носит имя её авторов Ч. Кобба и П. Дугласа.):

где Q — максимальный объем продукта при заданных факторах производства;

L, К — затраты труда, капитала;

k — коэффициент пропорциональности, или масштабности;

α, β — коэффициенты эластичности объема производства, со­ответственно, по труду и капиталу или коэффициенты прироста Q, приходящиеся на 1% прироста соответствующего фактора.

Названные коэффициенты в сумме измеряют совокупное про­центное изменение выпуска при данном процентном изменении затрат труда и капитала. Если а + Р = 1, то объём выпуска возрастает ровно на столько, на сколько увеличиваются затраты тру­да, капитала и материалов, имеет место постоянная отдача от масштаба, и функция Кобба-Дугласа в таком случае является однородной. Если (а + Р) > 1, то предприятием будет получена экономия от масштаба, свидетельствующая о том, что эффектив­ность факторов производства повышается в условиях техниче­ского прогресса. Если (а+Р) < 1, будет иметь место убывающая отдача от масштаба производства.