Изокванты

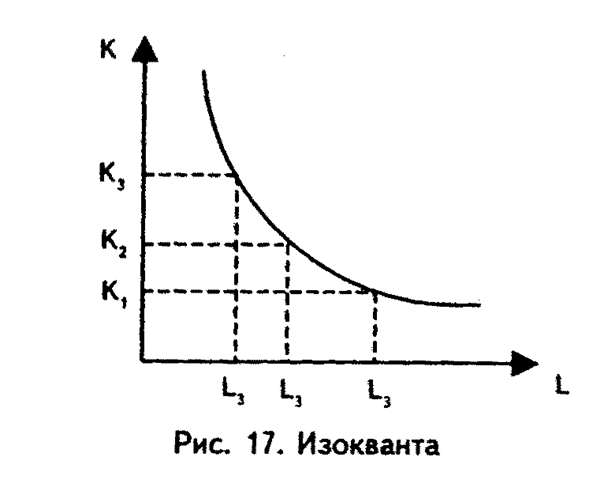
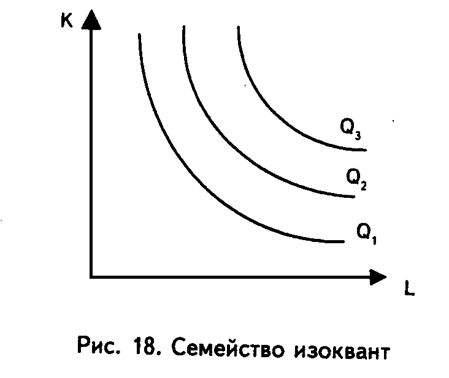
За редким исключением, конкретный продукт может быть произведен при использовании различных факторов производ­ства в изменяющихся пропорциях. Оставим пока в стороне слу­чаи, когда продукт можно произвести, используя факторы про­изводства только в одной пропорции, и когда никакое замеще­ние одного фактора другим невозможно. Другой крайний случай представляется ситуацией, когда используется бесконечное мно­жество эффективных комбинаций факторов. Тогда можно изме­нять на бесконечно малую величину затраты одного фактора и увеличивать на бесконечно малую величину затраты другого фактора для производства заданного объема продукции. Такая производственная функция является непрерывной. В последую­щем это свойство функции будем часто использовать. Между названными крайними случаями находятся промежуточные, ре­алистические, когда данное количество продукции можно про­извести с помощью определенного числа комбинаций факторов. Допустим, что в производстве продукта используются только два фактора — труд L и капитал К. Максимальный выпуск Q можно получить при сочетаниях факторов: (L_x, KJ, (L₂, K₂),..., (L, К_п), где п — любое положительное число. Построим кривую (рис. 17), каждой точке которой соответствует одно из сочетаний факторов. Это изокванта. На ней расположены все сочетания факторов производства, использование которых позволяет полу­чить один и тот же объем продукции Q. Изокванта показывает, что объем продукции Q можно произвести при небольших затра­тах труда L₃ и больших затратах капитала К₃, при небольших затратах капитала К₁ и больших затратах труда L_x и т.д. Таким образом, производственная функция графически представляется изоквантой.

Производственную функцию для различных объемов произ­водства Q₁, Q₂, Q₃ представляют изоквантами, так получаем се­мейство изоквант (рис.18). Если Q₃> Q₂> Q_v то изокванта Q₃ лежит выше и правее Q₂, и ей соответствуют такие сочетания производственных факторов, которые обеспечивают больший, чем Q₂ выпуск продукции.

Аналогично: изокванта Q₂ лежит выше и правее Q,. Объемы Q₁. Q₂> Q₃ представляют собой максимальный выпуск продукции Для различных в каждом случае сочетаний труда и капитала. Кроме того, изокванты показывают три различных уровня про­изводства расположением друг относительно друга.

Изокванты не пересекаются и переход от одного выпуска Q_l к другому Q₂ возможен только тогда, когда не только изменяется сочетание затрат труда и капитала, но и когда изменяется величина этих затрат. При прочих равных условиях затраты на изок-ванте Q₂ больше затрат на изокванте Q_r Это свидетельствует о том, что при переходе от Q_t к Q₂ остается неизменной форма производственной функции Д а значит остается неизменным спо­соб преобразования, эффективность преобразования затрат в про­дукцию. Для обозначения такого процесса применяется термин «эффективность технологии», которая в данном случае остается неизменной.

Так как технология воплощена в производственной функции, то ее можно выразить и измерить параметрами функции. По­скольку речь идет не о конкретной, а о любой технологии, тех­нологии вообще, то она называется абстрактной технологией и описывается с помощью четырех характеристик производствен­ной функции. Рассмотренная эффективность технологии представляет первую ее характеристику.

Предпринимателю изокванта помогает выбрать при измене­нии факторных цен такие сочетания затрат ресурсов, которые позволяют минимизировать издержки производства и максими­зировать прибыль.