Задачи для самостоятельного решения. 4.1. Напряженность Н магнитного поля в центре кругового витка радиусом r = 10 см равна 20 А/м
4.1. Напряженность Н магнитного поля в центре кругового витка радиусом r = 10 см равна 20 А/м. Определить ток, текущий по витку. 4.2. По проводнику длиной 5 м течет ток I = 150 А. Определить магнитную индукцию B и напряженность Н в точке О, удаленной от концов проводника на расстояния 4 м и 3 м соответственно. 4.3. Определить индукцию магнитного поля в центре проволочной квадратной рамки со стороной а = 15 см, если по рамке течет ток I = 5 А. 4.4. Определить магнитную индукцию ВА на оси тонкого кругового проволочного витка радиусом R = 10 см, в точке, расположенной на расстоянии d = 20 см от центра кольца, если при протекании тока по кольцу в центре кольца В = 50 мкТл.
4.6. По двум бесконечно длинным прямым проводникам, расстояние между которыми d = 20 см, текут токи I1 = 40 А и I2 = 80 А в одном направлении. Определить магнитную индукцию В в точке А, удаленной от первого проводника на r1 = 12 см и от второго – на r 2 = 16 см. 4.7. По двум бесконечно длинным, прямым параллельным проводам текут одинаковые токи I = 50 А. Расстояние между проводами 15 см. Определить магнитную индукцию B в точке A, равноудаленной от проводов на расстояние d = 10 см. 4.8. По двум скрещенным под прямым углом бесконечно длинным проводам текут токи I и 2 I (I = 50 А). Определить магнитную индукцию B в точке A (рис. 4.12). Расстояние d = 20 см. 4.9. По двум бесконечно длинным проводам, скрещенным под прямым углом, текут токи I 1 и I 2 = 2 I 1 (I 1 = 100 А). Определить магнитную индукцию B в точке A, равноудаленной от проводов на расстояние d = 10 см (рис. 4.13).
4.10. По двум бесконечно длинным прямым проводникам, расстояние между которыми d = 30 см, текут токи I1 = 50 А и I2 = 30 А в противоположных направлениях. Определить магнитную индукцию в точке А, удаленной от первого проводника на r1 = 10 см и от второго – на r 2 = 40 см. 2) в точке C, удаленной от первого проводника на r1 = 10 см и от второго - на r 2 = 20 см. 4.11. По двум параллельным проводам длиной L = 5 м каждый текут одинаковые токи I = 250 А. Расстояние d между проводами равно 20 см. Определить силу F взаимодействия проводов.
4.13. По двум одинаковым квадратным плоским контурам со стороной a = 15 см текут токи I = 25 А в каждом. Определить силу F взаимодействия контуров, если расстояние d между соответственными сторонами контуров равно 5 мм. 4.14. По кольцу радиусом R течет ток. На оси кольца на расстоянии d = 1 м от его плоскости магнитная индукция B = 24нТл. Определить магнитный момент рm кольца с током. Считать R много меньшим d. 4.15. Тонкий провод длиной L = 20 см изогнут в виде полукольца и помещен в магнитное поле (B =10 мТл) так, что площадь полукольца перпендикулярна линиям магнитной индукции. По проводу пропустили ток I = 50 А. Определить силу F, действующую на провод. Подводящие провода направлены вдоль линий магнитной индукции. 4.16. Тонкое проводящее кольцо массой m = 3 г свободно подвешено на неупругой нити в магнитном поле. По кольцу течет ток I = 5 A Период Т малых крутильных колебаний относительно вертикальной оси равен 1,5с. Найти магнитную индукцию поля. 4.17. Тонкое проводящее кольцо с током I = 50 A помещено в однородное магнитное поле (B = 120 мТл). Плоскость кольца перпендикулярна линиям магнитной индукции. Радиус R кольца равен 20 см. Найти силу F, растягивающую кольцо. 4.18. Протон движется по окружности радиусом R = 1,2 см с линейной скоростью v = 106 м/с. Определить магнитный момент pm, создаваемый эквивалентным круговым током. 4.19. Электрон в атоме водорода движется вокруг ядра (протона) по окружности радиусом R = 53 пм. Определить магнитный момент pm эквивалентного кругового тока. 4.20 Электрон в атоме водорода движется вокруг ядра по круговой орбите некоторого радиуса. Зная заряд электрона и его массу, определите отношение магнитного момента pm эквивалентного кругового тока к величине момента импульса L орбитального движения электрона. Как направлены векторы pm и L? 4.21.Определить силу Лоренца F, действующую на электрон, влетевший со скоростью 4.22. Вычислить радиус R окружности, которую описывает протон в магнитном поле с индукцией В = 15 мТл, если скорость протона равна 2 Мм/с. 4.23. Электрон, ускоренный разностью потенциалов U = 0,5 кВ движется параллельно прямолинейному длинному проводнику на расстоянии r = 1 см от него. Определить силу, действующую на электрон, если через проводник пропускать ток I = 10 А. 4.24. Протон, ускоренный разностью потенциалов U = 0,5 кВ, влетая в однородное магнитное поле с магнитной индукцией В = 2 мТл, движется по окружности. Определить радиус этой окружности. 4.25.Электрон разгоняется электрическим полем на участке с разностью потенциалов 1кВ и влетает в однородное магнитное поле с индукцией В = 2 мТл в направлении, перпендикулярном линиям индукции. Определить радиус траектории и период обращения электрона в магнитном поле. 4.26. Два иона, имеющие одинаковые заряды и одинаковые кинетические энергии, но различные массы, влетели в однородное магнитное поле. Первый ион описал окружность радиусом 3 см, а второй – 1,5 см. вычислить отношение масс ионов 4.27. Заряженная частица, прошедшая ускоряющую разность потенциалов U =2 кВ, движется в однородном магнитном поле с индукцией B =15,1 мТл по окружности радиусом R = 1см. Определить отношение 4.28. Протон с кинетической энергией T =1 МэВ влетел в однородное магнитное поле перпендикулярно линиям индукции (B = 1 Тл). Какова должна быть минимальная протяженность 4.29. Электрон движется в однородном магнитном поле с индукцией B = 9 мТл по винтовой линии, радиус R которой равен 1 см и 4.30. Перпендикулярно магнитному полю с индукцией B = 0,1 Тл возбуждено электрическое поле напряженностью E = 100 кВ/м. Перпендикулярно обоим полям движется, не отклоняясь от прямолинейной траектории заряженная частица. Вычислить скорость 4.31. Какой заряд протекает по проводнику сопротивлением 20 Ом, имеющем форму квадрата со стороной 0,4 м и расположенном в однородном магнитном поле с индукцией 1Тл, перпендикулярной плоскости квадрата, при исчезновении магнитного поля? 4.32. Проволочный контур в виде окружности, находящийся в однородном магнитном поле, деформировали в квадрат, не изменяя ориентацию плоскости контура в пространстве. Во сколько раз уменьшится магнитный поток, пронизывающий площадь, ограниченную контуром? 4.33 Плоский контур площадью S = 30 см2 находится в однородном магнитном поле (В = 0,05 Тл). Определить магнитный поток Ф, пронизывающий контур, если плоскость его составляет угол 4.34. На длинный картонный каркас диаметром d = 5 см уложена однослойная обмотка (виток к витку) из проволоки диаметром D = 0,2 мм. Определить магнитный поток Ф, создаваемый таким соленоидом при силе тока I = 0,5 А. 4.35. Квадратный контур со стороной a = 10 см, в котором течет ток I = 6А, находится в магнитном поле (В = 0,8 Тл) под углом 4.36. Плоский контур с током I = 7 A свободно установился в однородном магнитном поле (В = 0,5 Тл). Площадь контура S = 180 см2. Поддерживая ток в контуре неизменным, его повернули относительно оси, лежащей в плоскости контура, на угол 4.37. Виток, в котором поддерживается постоянная сила тока I = 60 A, свободно установился в однородном магнитном поле (В = 20 мТл). Диаметр витка d = 10 см. Какую работу A нужно совершить для того, чтобы повернуть виток относительно оси, совпадающей с диаметром, на угол 4.38. В однородном магнитном поле перпендикулярно линиям индукции расположен плоский контур площадью S = 100 см2. Поддерживая в контуре постоянную силу тока I = 100 A, его переместили из поля в область пространства, где поле отсутствует. Определить магнитную индукцию B поля, если при перемещении контура была совершена работа A = 0,5 Дж. 4.39. Плоский контур с током I = 50 A расположен в однородном магнитном поле (В = 1,2 Тл) так, что нормаль к контуру перпендикулярна линиям магнитной индукции. Определить работу, совершаемую силами поля при медленном повороте контура около оси, лежащей в плоскости контура, на угол 4.40. Определить магнитный поток Ф, пронизывающий соленоид, если его длина L = 50 см и магнитный момент pm = 0,4 A∙м2. 4.41. Самолет летит горизонтально со скоростью 900 км/час. При этом на концах крыла самолета возникает разность потенциалов 0,6В. Вертикальная составляющая напряженности магнитного поля Земли равна 89А/м. Какой размах имеют крылья самолета? 4.42. В однородном магнитном поле с индукцией В =0,1 Тл движется проводник длиной l = 10 cм. Скорость движения проводника v =15 м/с и направлена перпендикулярно к магнитному полю. Найти индуцированную в проводнике ЭДС. 4.43. При полете вертолета плоскость вращения его винта составляет с горизонтом угол a = 30°. Винт радиусом R = 5 м вращается с частотой n =10 Гц. Найти разность потенциалов между центром и краем винта. Вертикальная компонента магнитного поля Земли В =0,5 мТл. 4.44. В однородное магнитном поле с индукцией В =0,3 Тл помещена прямоугольная рамка с подвижной стороной, длина которой l = 15 cм. Определить ЭДС индукции, возникающей в рамке, если ее подвижная сторона перемещается перпендикулярно линиям магнитной индукции со скоростью 10 м/с. 4.45. При равномерном возрастании индукции магнитного поля, перпендикулярного поперечному сечению проволочной катушки площадью S = 10 cм2, от 0 до 0,2 Тл за 0,001 с на ее концах возникло напряжение 100В. Сколько витков N имеет катушка? 4.46. В магнитном поле с индукцией В =0,05 Тл, вращается стержень длиной l = 1 м с угловой скоростью w = 20 рад/с. Ось вращения проходит через конец стержня и параллельна магнитному полю. Найти ЭДС индукции, возникающую на концах стержня. 4.47. В однородное магнитном поле с индукцией В =0,8 Тл равномерно вращается рамка с угловой скоростью w = 15 рад/с. Площадь рамки S = 120 cм2. Ось вращения находится в плоскости рамки и составляет угол a = 30° с направлением магнитного поля. Найти максимальную ЭДС индукции во вращающейся рамке. 4.48. Круговой проволочный виток площадью S = 0,01 м2 находится в однородном магнитном поле с индукцией В = 1 Тл. Плоскость витка перпендикулярна к направлению магнитного поля. Найти среднюю ЭДС индукции, возникающую в витке, при выключении поля в течение времени 10 мс. 4.49. Через катушку, индуктивность которой равна 200 мГн, протекает ток, изменяющийся по закону I = 2cos(3t). Определить закон изменения ЭДС индукции и максимальное значение ЭДС самоиндукции. 4.50. В соленоиде без сердечника, содержащем 1000 витков, при увеличении силы тока магнитный поток увеличился на 1 мВб. Определить среднюю ЭДС самоиндукции, возникающую в соленоиде, если изменение силы тока произошло за 1 с. 4.51. Определить, сколько витков проволоки, вплотную прилегающих друг к другу, диаметром 0,3 мм надо намотать на картонный цилиндр диаметром 1 см, чтобы получить однослойную катушку с индуктивностью 1 мГн? 4.52. По катушке индуктивностью L = 0,05Гн течет ток силой I = 0,5 А. При размыкании цепи сила тока изменяется практически до нуля за время 4.53. Сила тока в катушке равномерно увеличивается на DI = 0,2 А в 1 с. Индуктивность катушки L равна 0,01 Гн. Определите среднее значение ЭДС самоиндукции. 4.54. Индуктивность катушки L равна 0,05 Гн. По катушке протекает ток частотой 50 Гц, изменяющийся по синусоидальному закону. Определите среднюю ЭДС самоиндукции, возникающую за интервал Dt, в течение которого ток в катушке изменяется от минимального до максимального значения. Амплитудное значение силы тока I0 = 12А. 4.55. Источник тока замкнули на катушку сопротивлением R =10 Ом и индуктивностью L = 0,2 Гн. Через какое время сила тока в цепи достигнет 50 % максимального значения? 4.56. Источник тока замкнули на катушку сопротивлением R = 20 Ом. Через время t = 0,1 с сила тока I в катушке достигла 0,95 предельного значения. Определить индуктивность L катушки. 4.57. В электрической цепи, содержащей резистор сопротивлением R = 20 Ом и катушку индуктивностью L = 0,06Гн, течет ток I = 20 А. Определить силу тока I в цепи через 4.58. Цепь состоит из катушки индуктивностью L = 0,1 Гн и источника тока. Источник тока отключили, не разрывая цепи. Время, через которое сила тока уменьшится до 0,001 первоначального значения, равно t = 0,07 с. Определить сопротивление катушки. 4.59. К источнику тока с внутренним сопротивлением RИ = 2 Ом подключают катушку индуктивностью L = 0,5 Гн и сопротивлением R = 10 Ом. Найти время t, в течение которого ток в катушке, нарастая, достигнет значения, отличающегося от максимального на 1%. 4.60. Цепь состоит из катушки катушку индуктивностью L = 0,5 Гн и сопротивлением R = 10 Ом. Источник тока можно отключать не разрывая цепи. Определите время t в течение которого сила тока уменьшится до 0,001 первоначального значения. 4.61. Две катушки намотаны на один сердечник. Индуктивность первой катушки L1 = 2,5Гн, второй - L2 = 0,4 Гн. Определите сопротивление второй катушки, если за время D t = 0,02 c сила тока в первой катушке уменьшилась от I1 = 2,0 А до нуля, а сила тока во второй катушке составила I2 = 0,5 А. 4.62. Две катушки расположены на небольшом расстоянии одна от другой. Когда сила тока в первой катушке изменяется со скоростью 5 А/с, во второй катушке возникает ЭДС индукции ei = 0,5 В. Определить коэффициент взаимной индукции катушек. 4.63. Две катушки имеют взаимную индуктивность L12 = 5 мГн. В первой катушке ток изменяется по закону I = I0sinwt, где I0= 10 А, w =2p/Т и Т = 0,02 с. Определите максимальное значение ЭДС, индуцируемое во второй катушке. 4.64. Трансформатор с коэффициентом трансформации 0,2 понижает напряжение с 220 В до 10 В. При этом сила тока во вторичной обмотке равна 5А. Пренебрегая потерями энергии в первичной обмотке, определить сопротивление вторичной обмотки трансформатора. 4.65. Трансформатор, понижающий напряжение с 220 В до 6 В содержит в первичной обмотке N1= 2200 витков. Сопротивление вторичной обмотки R2 = 0,2 Ом. Пренебрегая сопротивлением первичной обмотки, определить число витков во вторичной обмотке трансформатора, если во внешнюю цепь передается мощность Р = 30 Вт. 4.66. Автотрансформатор понижает напряжение с 6 кВ до 220 В. В первичной обмотке трансформатора содержится 1000 витков. Сопротивление вторичной обмотки составляет 2 Ом, сопротивление внешней цепи равно 10 Ом. Пренебрегая сопротивлением первичной обмотки, определить число витков во вторичной обмотке трансформатора. 4.67. Длинный прямой соленоид, намотанный на немагнитный каркас, имеет N = 1000 витков и индуктивность L = 3 мГн. Какой магнитный поток Ф и какое потокосцепление Y создает соленоид при силе тока I = 1А? 4.68. Соленоид длиной 50 см и диаметром 0,8 см имеет 20000 витков медного провода и находится под постоянным напряжением. Определите время, в течение которого в обмотке соленоида выделится количество теплоты, равное энергии магнитного поля в соленоиде. 4.69.Через катушку, индуктивность которой L = 5 мГн, течет ток, изменяющийся по закону I = I0sinwt, где I0 = 10 А, w = 2p/Т и Т = 0,01 с. Найдите зависимость от времени энергии магнитного поля катушки и ее максимальное значение. 4.70. Индуктивность соленоида при длине 1 м и площади поперечного сечения 20 см2 равна 0,4 мГн. Определите силу тока в соленоиде, при которой объемная плотность энергии магнитного поля внутри соленоида равна 0,1 Дж/м3. 4.71. Принимая, что электрон в невозбужденном атоме водорода движется по круговой орбите радиусом r = 52,8 пм определить орбитальный механический момент электрона Le. 4.72. Вычислите спиновой момент импульса LS электрона и проекцию этого момента на направление внешнего магнитного поля LSZ. 4.73. В однородное магнитное поле вносится длинный вольфрамовый стержень. Молекулярные токи в стержне составляют 0,0173 часть от суммарного магнитного потока в стержне. Определить магнитную восприимчивость c вольфрама. 4.74. По обмотке соленоида индуктивностью L = 3мГн, находящемся в диамагнитной среде, течет ток I = 0,4A. Длина соленоида l = 45 cм, число витков N = 1000, площадь поперечного сечения S = 10 см2. Определите намагниченность J внутри соленоида. 4.75. По обмотке соленоида индуктивностью L = 5мГн, находящемся в диамагнитной среде, течет ток I = 0,4A. Длина соленоида l = 40 cм, площадь поперечного сечения S = 10 см2. Магнитная индукция внутри соленоида равна В = 2мТл. Определите число витков в обмотке. 4.76. Индукция магнитного поля в железном стержне В = 1,0 Тл, напряженность однородного магнитного поля в стержне Н= 400 А/м. Определите намагниченность стержня J. 4.77. По круговому контуру радиусом r = 20 см, погруженном в жидкий кислород, течет ток. Намагниченность в центре этого контура J = 29,75 мА/м. Магнитная восприимчивость жидкого кислорода c равна 3,4·10-3. Определите величину тока I. 4.78. Индукция магнитного поля в железном стержне В = 1,2 Тл, напряженность однородного магнитного поля в стержне Н = 800 А/м. Определите магнитную восприимчивость c железа. 4.79. На стальном не намагниченном кольце (торе), средний диаметр которого d = 30 см и площадь поперечного сечения S = 1,6 см2, имеется обмотка, содержащая N = 800 витков. К тороиду подключен баллистический гальванометр, сопротивление цепи которого R = 0,8 Ом. При включении по обмотке тороида тока I = 1,8 А через баллистический гальванометр прошел заряд q = 0,24 мКл. Определить напряженность поля Н внутри кольца, намагниченность J кольца, остаточную намагниченность стального кольца после исчезновения тока в обмотке. 4.80. Напряженность однородного магнитного поля в платине равна 10А/м. Определите магнитную индукцию поля, создаваемого молекулярными токами, если магнитная восприимчивость платины c равна 3,6·10-4. Приложение 1 ТАБЛИЦЫ ВАРИАНТОВ ДЛЯ ИДЗ Приложение 1
Таблица 1 – Номера задач по вариантам к ИДЗ № 2 для студентов заочной и заочно- сокращенной формы обучения,
|

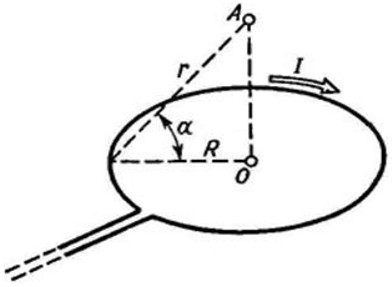 Рис. 4.11
Рис. 4.11
 Рис. 4.12
Рис. 4.12
 Рис. 4.13
Рис. 4.13
 Рис.4.14.
Рис.4.14.
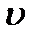 = 4 Мм/с в однородное магнитное поле под углом
= 4 Мм/с в однородное магнитное поле под углом  =30° к линиям индукции. Магнитная индукция поля равна 0,2 Тл.
=30° к линиям индукции. Магнитная индукция поля равна 0,2 Тл. /m заряда частицы к ее массе и скорость v частицы.
/m заряда частицы к ее массе и скорость v частицы. поля в направлении, по которому летел протон, когда он находился вне поля чтобы оно изменило направление движения протона на противоположное?
поля в направлении, по которому летел протон, когда он находился вне поля чтобы оно изменило направление движения протона на противоположное? = 60° с направлением линий индукции.
= 60° с направлением линий индукции. = 60° к линиям индукции. Какую работу A нужно совершить, чтобы при неизменной силе тока в контуре изменить его форму на окружность?
= 60° к линиям индукции. Какую работу A нужно совершить, чтобы при неизменной силе тока в контуре изменить его форму на окружность? /4?
/4? = 130 мкс. Определить среднюю ЭДС самоиндукции, возникающую в контуре.
= 130 мкс. Определить среднюю ЭДС самоиндукции, возникающую в контуре.


