Для экономических специальностей заочной формы обучения. 1. В первой урне находятся 1 белый и 4 черных шара, во второй урне – 2 белых и 3 черных шара, в третьей – 3 белых и 2 черных шара
Вариант 20 1. В первой урне находятся 1 белый и 4 черных шара, во второй урне – 2 белых и 3 черных шара, в третьей – 3 белых и 2 черных шара. Из каждой урны случайным образом вынули по одному шару. Найти вероятность того, что среди вынутых шаров будет один белый и два черных шара. 2. Система, состоящая из двух элементов типа А и трех элементов типа В, выходит из строя в случае, если отказывает хотя один элемент типа А или более одного элемента типа В. Найти надежность (вероятность безотказной работы) системы, если элементы независимы и вероятность безотказной работы элемента А равна 0,9, а элемента В равна 0,7. 3. В цехе три типа автоматов, которые производят одни и те же детали. Производительность их одинакова, но качество работы различно. Автоматы первого типа производят 90% деталей отличного качества, второго – 85%, третьего – 80%. Все детали в несортированном виде сложены на складе. Определить вероятность того, что взятая наудачу деталь отличного качества, если автоматов первого типа – 10 штук, второго – 8 штук, третьего – 2 штуки. 4. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа. а) Вероятность поражения мишени стрелком при одном выстреле равна 0,6. Найти вероятность того, что при 12 выстрелах мишень будет поражена 7 раз. б) Вероятность того, что деталь не прошла проверку ОТК, равна р =0,15. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных: 1) ровно80; 2) от 50 до 75. 5. Дискретная случайная величина Х имеет только два возможных значения: x 1 и x 2, причем x 1 < x 2. Вероятность того, что Х примет значение x 1 равно 0,9. Найти закон распределения Х, зная математическое ожидание М[ X ] = 2,3 и дисперсию D[ X ] = 0,81. 6. Непрерывная случайная величина Х задана функцией распределения
Найти: а) параметр k; б) математическое ожидание; в) дисперсию. 7. Известны математическое ожидание а =4 и среднее квадратичное отклонение s=2 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (3, 7); б) отклонения этой величины от математического ожидания не более, чем на d=3. 8. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда. а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительный интервал для математического ожидания с доверительной вероятностью g=0,95. б) Вычислить коэффициенты асимметрии и эксцесса, используя упрощенный метод вычислений, и сделать соответствующие предположения о виде функции распределения генеральной совокупности. в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости a=0,05.
9. Методом наименьших квадратов подобрать функцию
ВЫСШАЯ МАТЕМАТИКА Контрольная работа №3
|

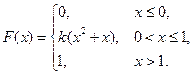
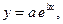 по табличным данным и сделать чертеж.
по табличным данным и сделать чертеж.


