Для экономических специальностей заочной формы обучения. 1. На полке в случайном порядке расставлено 10 книг, среди которых находится двухтомник Дж
Вариант 15 1. На полке в случайном порядке расставлено 10 книг, среди которых находится двухтомник Дж. Лондона. Найти вероятность того, что оба тома двухтомника расположены рядом. 2. Вероятность для данного спортсмена улучшить свой предыдущий результат с одной попытки равна 0,6. Определить вероятность того, что на соревнованиях спортсмен улучшит свой результат, если разрешается делать две попытки. 3. Три группы студентов одновременно сдают письменно зачет, причем в первой группе находится 27 человек, во второй – 18 человек, в третьей – 12. Известно, что в среднем с первой попытки сдают зачет в первой группе 75% студентов, во второй и третьей – 55% и 40%, соответственно. Наудачу взятая работа оказалась незачтенной. Какова вероятность того, что эта работа из первой группы? 4. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа. а) Вероятность получения удачного результата при производстве сложного химического опыта равна 2/3. Общее число опытов равно 5. Найти вероятность того, что не менее чем в 3-х опытах получится удачный результат. б) Вероятность поражения мишени стрелком при одном выстреле равна 0,85. Найти вероятность того, что при 90 выстрелах мишень будет поражена: 1) 75 раз; 2) не менее 73, но не более 83 раз. 5. Дан перечень возможных значений дискретной случайной величины Х: x 1=–3, x 2=2, x 3=3, а также даны математическое ожидание этой величины M[ X ]=1,8 и ее квадрата M[ X 2]=6. Найти закон распределения случайной величины Х. 6. Непрерывная случайная величина Х задана функцией распределения
Найти: а) параметр k; б) математическое ожидание; в) дисперсию. 7. Известны математическое ожидание а =2 и среднее квадратичное отклонение s=5 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (6, 11); б) отклонения этой величины от математического ожидания не более, чем на d=4. 8. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда. а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительный интервал для математического ожидания с доверительной вероятностью g=0,95. б) Вычислить коэффициенты асимметрии и эксцесса, используя упрощенный метод вычислений, и сделать соответствующие предположения о виде функции распределения генеральной совокупности. в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости a=0,05.
9. Методом наименьших квадратов подобрать функцию
ВЫСШАЯ МАТЕМАТИКА Контрольная работа №3
|

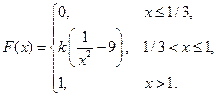
 по табличным данным и сделать чертеж.
по табличным данным и сделать чертеж.


