Для экономических специальностей заочной формы обучения. 1. Собрание, на котором присутствуют 25 человек, в том числе 15 женщин, выбирают делегацию из 5 человек
Вариант 12 1. Собрание, на котором присутствуют 25 человек, в том числе 15 женщин, выбирают делегацию из 5 человек. Найти вероятность того, что в делегацию войдут 3 женщины, считая, что каждый из присутствующих может быть избран с одинаковой вероятностью. 2. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,26. Найти вероятность поражения цели первым из орудий, если известно, что вероятность попадания в цель вторым орудием при одном выстреле равна 0,9. 3. В двух ящиках имеются радиолампы. В первом ящике содержится 12 ламп, из них 1 нестандартная; во втором 10 ламп, из них 1 нестандартная. Из первого ящика наудачу взята лампа и переложена во второй. Найти вероятность того, что наудачу извлеченная лампа из второго ящика лампа будет нестандартной. 4. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа. а) Каждое утро студент может опоздать на занятия с вероятностью 0,1. Сколько дней потребуется студенту, чтобы вероятность опоздания на занятия была равна 0,99. б) Вероятность выхода из строя одного прибора равна 0,15. Найти вероятность того, что из 90 имеющихся приборов выйдет из строя: 1) ровно 10, 2) больше 15, но меньше 20. 5. Дан перечень возможных значений дискретной величины Х: x 1=1, x 2=2, x 3=3, а также даны математическое ожидание этой величины M[ X ]=2,3 и ее квадрата M[ X 2]=5,9. Найти закон распределения случайной величины Х. 6. Непрерывная случайная величина Х задана функцией распределения
Найти: а) параметр k; б) математическое ожидание; в) дисперсию. 7. Известны математическое ожидание а =3 и среднее квадратичное отклонение s=2 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (2, 5); б) отклонения этой величины от математического ожидания не более, чем на d=3. 8. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда. а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительный интервал для математического ожидания с доверительной вероятностью g=0,95. б) Вычислить коэффициенты асимметрии и эксцесса, используя упрощенный метод вычислений, и сделать соответствующие предположения о виде функции распределения генеральной совокупности. в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости a=0,05.
9. Методом наименьших квадратов подобрать функцию
ВЫСШАЯ МАТЕМАТИКА Контрольная работа №3
|

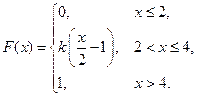
 по табличным данным и сделать чертеж.
по табличным данным и сделать чертеж.


