Приклади виконання роботи.
Пример 1. Упростить выражение: a2 – b2 . 2a + 2b Решение. В окне редактирования (далее на экране) набираем исходное выражение Указатель мыши подводим к опции “Символы” в главном меню и щелкаем левой кнопкой мыши один раз (далее входим в “Символы”). В выпавшем меню указатель мыши подводим к опции “Упростить” и активизируем (щелчком левой кнопкой мыши) указанную опцию. На экране отображается наше выражение, но уже в выделенном виде. Повторяем наши действия: входим в “Символы” (подводим указатель мыши и щелкаем левой кнопкой мыши) и активизируем “Упростить”. На экране появляется ответ: Пример 2. Вычислить: 10x2 –5y2, при x=1,5 и y=-1,6. Решение. На экране набираем; с клавиатуры набираем знак =, компьютер сам поставит знак:=. x: =1.5 y: =-1.6 10. x2 – 5. y2= рядом со знаком равенства читаем ответ: 9.7. Пример 3. Преобразуйте в многочлен: (a + 2. b) . (a – 2. b) . (a2 + 4. b2). Решение. На экране набираем исходное выражение (a + 2. b) . (a – 2. b) . (a2 + 4. b2) Входим в меню “Символы”, активизируем “Расширить”. На экране читаем ответ: a4 – 16. b4. Пример 4. Разложите на множители: 4z4 – 25k2. Решение. На экране набираем 4.z4 – 25.k2 Входим в меню “Символы”, активизируем “Фактор”. На экране читаем ответ: -(5.k – 2.z2).(5.k2 + 2.z2). Пример 5. Разложите на множители: 12x3 – 3x2y – 18xy2. Решение. На экране набираем 12. x3 – 3. x2. y – 18. x. y2. Входим в меню “Символы”, активизируем “Фактор”. На экране читаем ответ: 3. (4. x2 – x. y –6 . y2).
Пример 6. Сократите дробь: x2 – 2. m. x + 3. x - 6. m. x2 + 2. m. x + 3. x + 6. m Решение. На экране набираем исходное выражение. Входим в меню “Символы”, активизируем “Упростить”. На экране читаем ответ: (x – 2. m). (x + 2. m) Пример 7. Вычислите: 36-1/2. 271/3 – 811/4 . 5 Решение. На экране набираем искомый пример. Ставим знак равенства и читаем ответ: -0. 014.
Пример 8. Решите уравнение: 2. (5. x – 1)2 + 35. x – 11 = 0. Решение. Аналитическое решение. Набираем ключевое слово given (дано). Вводим уравнение 2. (5. x – 1)2 + 35. x – 11 = 0. Здесь при вводе знака =, мы вводим знак - логическое равно из палитры, а не с клавиатуры. Набираем find(x)à;, рядом читаем решение: - 33 5 10 Пример 9. Решите уравнение: y3 + 6. y2 – 16. y = 0. Решение. Численный поиск корней уравнения. Для поиска корней искомой переменной, надо присвоить начальное значение, а затем при помощи вызова функции root(f(x),x) находим корень. Набираем на экране y:=1 root(y3 + 6. y2 – 16. y, y)= читаем ответ: -8. Если в качестве начального значения возьмем y:=-2, то получим ответ: 0. Пример 10. Решите систему уравнений: x2 + y +8 = x. y y – 2. x = 0. Решение. Набираем ключевое слово given и систему уравнений x2 + y +8 = x. y y – 2. x = 0. Между левыми и правыми частями уравнений ставим знак логическое равно =. Набираем вызов функции find(x,y)à;, читаем на экране ответ: -2 4 -4 8 Пример 11. а) Решите неравенство: 5. x – 3 =< 4. Решение. На экране набираем неравенство и входим в палитру “Символические операторы”, активизируем “ solve”, набираем x 5. x – 3 =< 4 solve, x à на экране читаем ответ: x=< 7/5. б) Решите неравенство: 2. a2 – 5 < 15. На экране набираем неравенство и входим в палитру “Символические операторы”, активизируем “ solve”, набираем а 2. a2 – 5 < 15 solve, a à на экране читаем ответ:(- Пример 12. Вычислите: cos 340 . cos 560 – sin 340 .sin 1240. Решение. Набираем на экране cos (34 . deg) . cos (56 . deg) – sin (34 . deg) . sin (124 . deg)= и читаем ответ: 0. Примечание. Набираем deg, если угол задан в градусах; rad – в радианах. Пример 13. Построить график функции y=2 . sin 2. x. Решение. Набираем на экране y(x):=2 . sin (2. x). Отводим указатель мыши от выделенной части и щелкаем левой кнопкой мышки. Указатель мыши подводим к “Построение графиков” и входим, активизируем “Декартов график”. Появляется шаблон для построения графика. На ней выделены метки. Указатель мыши подводим к нижней метке, активизируем. Набираем x. Появляются по горизонтали еще две метки, где мы должны указать интервалы построения графика. Указатель мыши подводим к левой метке, щелкая левой кнопкой мыши активизируем и вводим левую границу 0. Указатель мыши подводим к правой границе, активизируем и вводим 5. Уводим указатель мыши к метке оси Y, активизируем его и вводим y(x). Появляются метки нижней и верней границ оси Y. В нижней набираем –2, в верхней 2. Отводим указатель мыши от шаблона для графиков, щелкаем левой кнопкой мыши. Появляется искомый график. Для форматирования графика нужно дважды щелкнуть в области графика. В выпавшем меню
можно управлять отображением линий, масштабом и др.
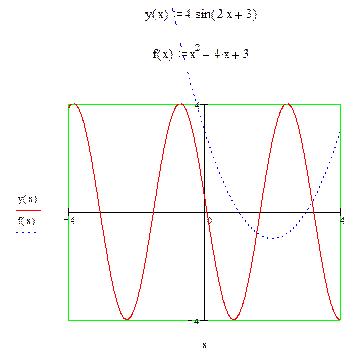
Пример 14. Построить графики функций: y(x)=4sin(2 x +3) и f(x)=x2-4x+3. Решение. Решение аналогично предыдущему примеру. В шаблоне для построения графиков имена функций набираем через запятую. Ограничений для значений аргументов и функций не ставим. Далее щелкаем мышью вне поля графиков.
Пример 15. Построить график функций z=sin(x2+y2) для x от –2 до 2 и y от –2 до 2. Фрагмент выполнения задания приведен ниже.
Пример 16. Вычислите предел многочлена: 2. x3 – 3. x2 +3. Решение. Из палитры “Высшей математики”, активизируем lim, заполняем выведенный шаблон; завешаем набор знаком à палитры “Операторы отношений”. На экране читаем ответ: 7. Пример 17. Вычислите производную: cos x + x. sin x. Решение. Из палитры “Высшей математики”, активизируем Пример 18. Вычислите неопределенный интеграл: Решение. Из палитры “Высшей математики”, активизируем Пример 19. Вычислите определенный интеграл: Решение Из палитры “Высшей математики”, активизируем Контрольні запитання 1. За допомогою якого оператора можна обчислити вирази? 2. Як вставити текстову область у документ Mathcad? 3. Чим відрізняється глобальне і локальне визначення змінних? За допомогою яких операторів вони визначаються? 4. Як змінити формат чисел для всього документа? 5. Як змінити формат чисел для окремого виразу? 6. Які системні (визначені) змінні Вам відомі? Як довідатися про їхнє значення? Як змінити їхнє значення? 7. Які види функцій у Mathcad Вам відомі? 8. Як вставити вбудовану функцію в документ Mathcad? 9. За допомогою яких операторів можна обчислити інтеграли, похідні, суми і добутки? 10. Як визначити дискретні змінні з довільним кроком? Який крок за замовчуванням? 11. Як визначити індексовану змінну? 12. Які види масивів у Mathcad Вам відомі? 13. Яка системна змінна визначає нижню границю індексації елементів масиву? 14. Опишіть способи створення масивів у Mathcad. 15. Як переглянути зміст масиву, визначеного через дискретний аргумент? 16. Як побудувати графіки: поверхні; полярний; декартовий? 17. Як побудувати декілька графіків в одній системі координат? 18. Як змінити масштаб графіка? 19. Як визначити координату точки на графіку? 20. Як побудувати гістограму? 21. Які функції використовуються для побудови тривимірних графіків? 22. Як створити анімацію в Mathcad? 23. Яке розширення мають збережені файли анімацій? Вправи для самостійної роботи. Вправа 1. Обчислити:
Це і всі інші завдання доповнити коментарями, використовуючи команду Вставка Þ Текстова область. Вправа 2. Визначити змінні: a:= 3.4, b:= 6.22, c º 0.149 (причому змінну з - глобально) і вирази:
· Обчислити вирази. · За допомогою команди ФорматÞРезультатÞФормат чиселÞЧисло знаків змінити точність відображення результатів обчислення глобально. Вправа 3. Вивести на екран значення системної константи p і встановити максимальний формат її відображення локально. Вправа 4. Виконати наступні операції з комплексними числами: Z:= -3 + 2 i |Z| = Re (Z) = Im (Z) = arg (Z) =
Z 1 + Z 2 = Z 1 - Z 2 = Z 1× Z 2 = Z 1 /Z 2 = Вправа 5. Виконати наступні операції: i: = 1.. 10
Вправа 6. Визначити вектори d, S і R через дискретний аргумент i. Відобразити графічно таблично задані функції Si (di) і Ri (di), використовуючи команду ВставкаÞГрафікÞX-Y Залежність.
Щоб оформити графік, необхідно виконати наступні команди: · Клацнути лівою клавішею миші на графіку, щоб виділити його. Потім клацнути правою клавішею миші, при цьому з'явиться контекстне меню в який необхідно вибрати команду Формат (з'явиться діалогове вікно “Formatting Currently Selected X-Y Plot”). · Нанести лінії сітки на графік (Осі X-Y ÞВспом. лінії) і відобразити легенду(СлідÞСховати легенду) · Відформатувати графік так, щоб у кожній вузловій точці графіка функції Si (di) стояв знак виду (СлідÞСимволÞbox), а графік функції Ri (di) відобразити у виді гістограми (СлідÞТипÞbar). Вправа 7. Побудувати у декартових (X-Y Залежність) і полярних (Полярні Координати) графіки наступних функцій:
Для цього необхідно визначити a як дискретний аргумент на інтервалі від 0 до 2×p із кроком p/30. Визначити за графіком X-Y Залежність координати кожної з точок перетинання графіків Y (a) і P (a), для цього необхідно: · Виділити графік і вибрати з контекстного меню Масштаб (з'явиться діалогове вікно “X-Y Zoom”) для збільшення частини графіка в області точки перетинання. · На кресленні виділити пунктирним прямокутником околицю точки перетинання графіків Y (a) і P (a), яку потрібно збільшити. · Натиснути кнопку Масштаб+, щоб перемалювати графік. · Щоб зробити це зображення постійним, вибрати ОК. · Вибрати з контекстного меню Трасування (з'явиться діалогове вікно “X‑ Y Trace”). · Всередині креслення натиснути кнопку миші і перемістити курсор миші на точку, чиї координати потрібно побачити. · Вибрати Copy X (чи Copy Y), на вільному полі документа набрати Xper:= (чи Yper:=) і вибрати пункт меню ВиправленняÞВставка. Обчислити значення функцій Х (a) і Y (a) при a:=p¤2. Вправа 8. Використовуючи команду ВставкаÞМатриця створити матрицю Q розміром 6´6, заповнити її довільно і відобразити графічно за допомогою команди ВставкаÞГрафікÞПоверхні. Вправа 9. Побудувати графік поверхні (Поверхневий) і карту ліній рівня (Контурний) для функції двох змінних
1. За допомогою функції CreateMesh (сітка розміром 40 ´ 40, діапазон зміни t від –5 до 5, a - від 0 до 2×p). 2. Задавши поверхню математично, для цього: · Визначити функцію X (t,a) · Задати на осях змінних t і a по 41 точці i: = 0..40 j: = 0..40 для змінної ti зі значеннями, що змінюються від -5 до 5 із кроком 0.25 ti:= - 5 + 0.25 × i, а для змінної a j - від 0 до 2×p із кроком p/20a j:= p/20 × j. · Визначити матрицю Мi j:= X (ti,a j) і відобразити її графічно. За допомогою команди Формат контекстного меню викликати діалогове вікно“ Формат 3-D графіка” ізмінити: · характеристики перегляду (ЗагальнеÞВидÞОбертання, Нахил), · кольори і лінії поверхні (Зовнішній ВиглядÞВластивості лінії, Властивості заливання), · параметри осей (Осі), · вид заголовка графіка (Назва). Вправа 10. Відобразити графічно перетинання поверхонь
|

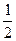 a -
a - 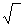 10<a). (a<
10<a). (a< 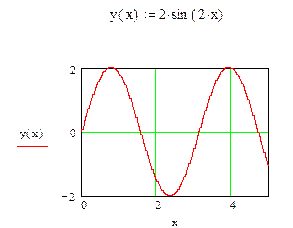

 , заполняем выведенный шаблон; завешаем набор знаком à палитры “Операторы отношений”. На экране читаем ответ: x. cos(x).
, заполняем выведенный шаблон; завешаем набор знаком à палитры “Операторы отношений”. На экране читаем ответ: x. cos(x).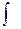 (x2 + cos x)dx.
(x2 + cos x)dx.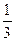 x3 + sin(x.)
x3 + sin(x.)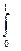
 ,заполняем выведенный шаблон; завешаем набор знаком à; палитры “Операторы отношений”. На экране читаем ответ:
,заполняем выведенный шаблон; завешаем набор знаком à; палитры “Операторы отношений”. На экране читаем ответ: 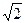 -
- 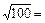 |-10| = 10! =.
|-10| = 10! =.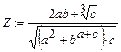
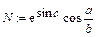 .
. =
= 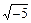 = 2 × Z = Z 1:=1 + 2 i Z 2: = 3 + 4 i
= 2 × Z = Z 1:=1 + 2 i Z 2: = 3 + 4 i =
= 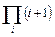 =
= 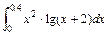 =
=  = x:=2
= x:=2 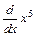 =
=  =
=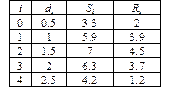
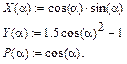
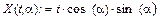 , двома способами:
, двома способами: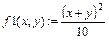 і
і 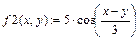 . Матриці для побудови поверхонь задати за допомогою функції CreateMesh, значення факультативних параметрів не вказувати. Виконати однотонне заливання для поверхонь, вибравши з контекстного меню команду Формат. Також з контекстного меню вибрати ефекти Туман, Висвітлення, Перспектива.
. Матриці для побудови поверхонь задати за допомогою функції CreateMesh, значення факультативних параметрів не вказувати. Виконати однотонне заливання для поверхонь, вибравши з контекстного меню команду Формат. Також з контекстного меню вибрати ефекти Туман, Висвітлення, Перспектива.


