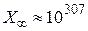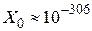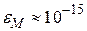Задача 1.6. Постановка задачи: для пакета MATHCAD найти значения машинного нуля, машинной бесконечности, машинного эпсилон.
Теоретический материал. ВЭВМ для вещественных чисел используется двоичная система счисления и принята форма представления чисел с плавающей точкой  ,
,  . Здесь
. Здесь  - мантисса;
- мантисса;  - двоичные цифры, причем всегда
- двоичные цифры, причем всегда  =1, p-целое число называемое двоичным порядком. Количество t цифр, которое отводится для записи мантиссы, называется разрядностью мантиссы. Диапазон представления чисел в ЭВМ ограничен конечной разрядностью мантиссы и значением числа p. Все представимые числа на ЭВМ удовлетворяют неравенствам:
=1, p-целое число называемое двоичным порядком. Количество t цифр, которое отводится для записи мантиссы, называется разрядностью мантиссы. Диапазон представления чисел в ЭВМ ограничен конечной разрядностью мантиссы и значением числа p. Все представимые числа на ЭВМ удовлетворяют неравенствам:  , где
, где  ,
,  . Все числа, по модулю большие
. Все числа, по модулю большие  , не представимы на ЭВМ и рассматриваются как машинная бесконечность. Все числа, по модулю меньшие
, не представимы на ЭВМ и рассматриваются как машинная бесконечность. Все числа, по модулю меньшие  , для ЭВМ не отличаются от нуля и рассматриваются как машинный нуль. Машинным эпсилон
, для ЭВМ не отличаются от нуля и рассматриваются как машинный нуль. Машинным эпсилон  называется относительная точность ЭВМ, то есть граница относительной погрешности представления чисел в ЭВМ. Покажем, что
называется относительная точность ЭВМ, то есть граница относительной погрешности представления чисел в ЭВМ. Покажем, что  . Пусть
. Пусть  , тогда граница абсолютной погрешности представления этого числа равна
, тогда граница абсолютной погрешности представления этого числа равна  . Поскольку
. Поскольку 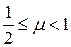 , то величина относительной погрешности представления оценивается так:
, то величина относительной погрешности представления оценивается так:
 .
.
Машинное эпсилон определяется разрядностью мантиссы и способом округления чисел, реализованным на конкретной ЭВМ.
Примем следующие способы определения приближенных значений параметров, требуемых в задаче:
1. Положим 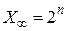 , где n - первое натуральное число, при котором происходит переполнение.
, где n - первое натуральное число, при котором происходит переполнение.
2. Положим  , где m – первое натуральное число, при котором
, где m – первое натуральное число, при котором 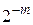 совпадает с нулем.
совпадает с нулем.
3. Положим  , где k – наибольшее натуральное число, при котором сумма вычисленного значения 1+
, где k – наибольшее натуральное число, при котором сумма вычисленного значения 1+  еще больше 1. Фактически
еще больше 1. Фактически  есть граница относительной погрешности представления числа
есть граница относительной погрешности представления числа  .
.
Результаты вычислительного эксперимента:
Машинная бесконечность 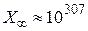
Машинный нуль 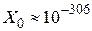
Машинное эпсилон 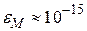
Tексты программ:




 ,
,  . Здесь
. Здесь  - мантисса;
- мантисса;  - двоичные цифры, причем всегда
- двоичные цифры, причем всегда  =1, p-целое число называемое двоичным порядком. Количество t цифр, которое отводится для записи мантиссы, называется разрядностью мантиссы. Диапазон представления чисел в ЭВМ ограничен конечной разрядностью мантиссы и значением числа p. Все представимые числа на ЭВМ удовлетворяют неравенствам:
=1, p-целое число называемое двоичным порядком. Количество t цифр, которое отводится для записи мантиссы, называется разрядностью мантиссы. Диапазон представления чисел в ЭВМ ограничен конечной разрядностью мантиссы и значением числа p. Все представимые числа на ЭВМ удовлетворяют неравенствам:  , где
, где  ,
,  . Все числа, по модулю большие
. Все числа, по модулю большие  , не представимы на ЭВМ и рассматриваются как машинная бесконечность. Все числа, по модулю меньшие
, не представимы на ЭВМ и рассматриваются как машинная бесконечность. Все числа, по модулю меньшие  , для ЭВМ не отличаются от нуля и рассматриваются как машинный нуль. Машинным эпсилон
, для ЭВМ не отличаются от нуля и рассматриваются как машинный нуль. Машинным эпсилон  называется относительная точность ЭВМ, то есть граница относительной погрешности представления чисел в ЭВМ. Покажем, что
называется относительная точность ЭВМ, то есть граница относительной погрешности представления чисел в ЭВМ. Покажем, что  . Пусть
. Пусть  , тогда граница абсолютной погрешности представления этого числа равна
, тогда граница абсолютной погрешности представления этого числа равна  . Поскольку
. Поскольку 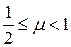 , то величина относительной погрешности представления оценивается так:
, то величина относительной погрешности представления оценивается так: .
.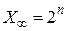 , где n - первое натуральное число, при котором происходит переполнение.
, где n - первое натуральное число, при котором происходит переполнение. , где m – первое натуральное число, при котором
, где m – первое натуральное число, при котором 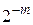 совпадает с нулем.
совпадает с нулем. , где k – наибольшее натуральное число, при котором сумма вычисленного значения 1+
, где k – наибольшее натуральное число, при котором сумма вычисленного значения 1+  еще больше 1. Фактически
еще больше 1. Фактически  .
.