Решение системы методом Крамера
Порядок выполнения работы.
1. Вычисляем D определитель матрицы А. 2. Зададим матрицу DX1, заменой первого столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX1. 3. Зададим матрицу DX2, заменой второго столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX2. 4. Зададим матрицу DX3, заменой третьего столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX3. 5. Определяем решение системы линейных уравнений x1, x2, x3.
Решение системы линейных алгебраических уравнение методом простых итераций Порядок выполнения задания 1. Введите матрицы C и d. 2. Преобразуйте исходную систему Cx=d к виду x=b+Ax. 3. Определите нулевое приближение решения. 4. Задайте количество итераций. 5. Вычислите последовательные приближения.
6.Решение системы линейных алгебраических уравнений методом Зейделя Порядок выполнения задания 1. Введите матрицы С и d. 2. Преобразуйте систему Cx=d к виду x=b+A1x+A2x. 3. Определите нулевое приближение решения. 4. Задайте количество итераций. 5. Вычислите последовательные приближения.
Таблица 2
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. К какому типу - прямому или итерационному - относится метод Гаусса? 2. В чем заключается прямой и обратный ход в схеме единственного деления? 3. Как организуется, контроль над вычислениями в прямом и обратном ходе? 4. Как строится итерационная последовательность для нахождения решения системы линейных уравнений? 5. Как формулируется достаточные условия сходимости итерационного процесса? 6. Как эти условия связаны с выбором метрики пространства? 7. В чем отличие итерационного процесса метода Зейделя от аналогичного процесса метода простой итерации?
Лабораторная работа №5 Тема: Интерполирование функций Мета: закріплення теоретичних знань; набуття практичних навичок обчислення у роботі В MATHCAD Робоче місце: учбове місце в кабінеті (комп’ютерний клас) Тривалість заняття: 90 хв. Метеріально-технічне оснащення: методичні вказівки, комп’ютер Хід роботи
Пусть функция Классический подход к решению задачи построения приближающей функции основывается на требование строгого совпадения значений
В этом случае нахождение приближенной функции называют интерполяцией (или интерполированием), точки Часто интерполирование ведется для функций, заданных таблицами с равноотстоящими значениями аргумента
|








 задана таблично, либо вычисление ее требует громоздких выкладок. Заменим приближенно функцию
задана таблично, либо вычисление ее требует громоздких выкладок. Заменим приближенно функцию 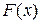 , так, чтобы отклонение
, так, чтобы отклонение  и
и  (
(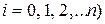 , т. е.
, т. е. . (3.1)
. (3.1) – узлами интерполяции.
– узлами интерполяции. . В этом случае шаг таблицы
. В этом случае шаг таблицы 
 является величиной постоянной. Для таких таблиц построение интерполяционных формул (как, впрочем, и вычисление по этим формулам) заметно упрощается.
является величиной постоянной. Для таких таблиц построение интерполяционных формул (как, впрочем, и вычисление по этим формулам) заметно упрощается.


