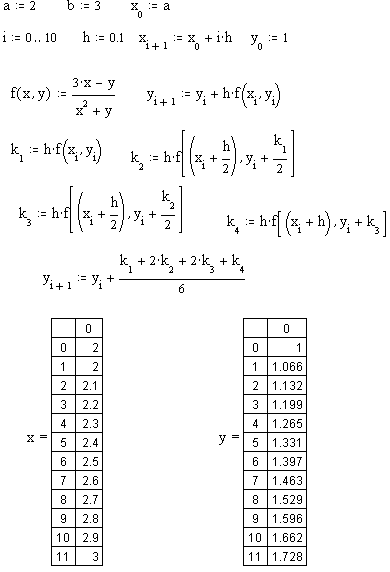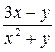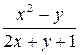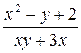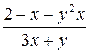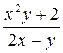Задание 2. Написать программу решения дифференциального уравнения методом Рунге-Кутта на отрезке с шагом и 2h и началь
Написать программу решения дифференциального уравнения
Примерный фрагмент выполнения лабораторной работы 1. Решить дифференциальное уравнение y’=f(x,y) методом Эйлера на отрезке [a,b] с шагом h c начальным условием y(a)=y0 , f(x,y)=(3x-y)/(x2+y), a=2, b=3, h=0.1, y0=1.
2. Решить дифференциальное уравнение y’=f(x,y) методом Рунге-Кутта на отрезке [a,b] с шагом h c начальным условием y(a)=y0.
Таблица 5
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Проверить для дифференциального уравнения условия теоремы существования и единственности. 2. На какие основные группы подразделяются приближенные методы решения дифференциальных уравнений? 3. В какой форме можно получить решение дифференциального уравнения по методу Эйлера? 4. Каков геометрический смысл решения дифференциального уравнения методом Эйлера? 5. В какой форме можно получить решение дифференциального уравнения по методу Рунге-Кутта? 6. Какой способ оценки точности используется при приближенном интегрировании дифференциальных уравнений методами Эйлера и Рунге-Кутта? 7. Как вычислить погрешность по заданной формуле, используя метод двойного пересчета?
|
методом Рунге-Кутта на отрезке 
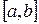с шагом 
и 2h и начальным условием 
. Оценить погрешность по формуле (5.5). Исходные данные для выполнения задания берутся из таблицы 5.
