Лабораторная работа №7. Тема: Численное решение дифференциальных уравнений
Тема: Численное решение дифференциальных уравнений Мета: закріплення теоретичних знань; набуття практичних навичок обчислення у роботі В MATHCAD Робоче місце: учбове місце в кабінеті (комп’ютерний клас) Тривалість заняття: 90 хв. Метеріально-технічне оснащення: методичні вказівки, комп’ютер Хід роботи Пусть дано дифференциальное уравнение первого порядка
Требуется найти на отрезке
Будем предполагать, что условия теоремы существования и единственности выполнены. Для решения используем метод Эйлера (метод первого порядка точности, расчетные формулы (5.3)) и метод Рунге-Кутта (метод четвертого порядка точности, расчетные формулы (5.4)) с шагом h и 2h. Отметим, что результаты могут сильно отличаться, ввиду того, что метод Эйлера, имея только первый порядок точности, используется, как правило, для оценочных расчетов. Ориентировочную оценку погрешности метода Рунге-Кутта
Задание 1 Написать программу решения дифференциального уравнения
|

 . (5.1)
. (5.1) решение
решение  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию (5.2)
(5.2) вычислить по формуле (5.5) [2].
вычислить по формуле (5.5) [2]. , где h – шаг разбиения. (5.3)
, где h – шаг разбиения. (5.3) , где (5.4)
, где (5.4)
 .
.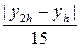 (5.5)
(5.5) методом Эйлера на отрезке
методом Эйлера на отрезке  и 2h и начальным условием
и 2h и начальным условием  . Исходные данные для выполнения задания берутся из таблицы 5. Сравнить результаты.
. Исходные данные для выполнения задания берутся из таблицы 5. Сравнить результаты.


