В задачах 1.9 и 1.10 исходный вопрос решается путем нахождения определителя и сравнения его с нулем. В случае, когда элементы определителя заданы точно, следует вычислить определитель и правильно ответить на поставленный в задаче вопрос.
В случае, когда элементы определителя заданы приближенно с относительной погрешностью d, дело обстоит сложнее. Пусть элементы матрицы обозначены через  . Тогда каждый элемент матрицы
. Тогда каждый элемент матрицы  теперь уже не равен конкретному значению, а может принимать любое значение из oтрезка [
теперь уже не равен конкретному значению, а может принимать любое значение из oтрезка [  (1 - d);
(1 - d);  (1 + d) ], если
(1 + d) ], если  > 0, и из отрезка [
> 0, и из отрезка [  (1 + d);
(1 + d);  (1 - d) ], если
(1 - d) ], если  < 0. Множество всех возможных значений элементов матрицы представляет собой замкнутое ограниченное множество в 9-мерном пространстве. Сам определитель является непрерывной и дифференцируемой функцией 9 переменных - элементов матрицы
< 0. Множество всех возможных значений элементов матрицы представляет собой замкнутое ограниченное множество в 9-мерном пространстве. Сам определитель является непрерывной и дифференцируемой функцией 9 переменных - элементов матрицы  . По известной теореме Вейерштрасса эта функция достигает на указанном множестве своего наибольшего и наименьшего значений M и m. Если отрезок [ m, M ] не содержит точку 0, то это означает, что при всевозможных допустимых значениях элементов матрицы
. По известной теореме Вейерштрасса эта функция достигает на указанном множестве своего наибольшего и наименьшего значений M и m. Если отрезок [ m, M ] не содержит точку 0, то это означает, что при всевозможных допустимых значениях элементов матрицы  определитель не обращается в 0. Если же точка 0 принадлежит отрезку [ m, M ], такое утверждение будет неправомерным. Будет иметь место неопределённость.
определитель не обращается в 0. Если же точка 0 принадлежит отрезку [ m, M ], такое утверждение будет неправомерным. Будет иметь место неопределённость.
Нахождению значений m и M помогают следующие рассуждения. Как функция своих аргументов (элементов матрицы  ) определитель обладает таким свойством (принцип максимума): эта функция достигает своего наибольшего и наименьшего значений всегда на границе области. Более того, можно доказать, что эти значения достигаются в точках, координаты которых имеют вид
) определитель обладает таким свойством (принцип максимума): эта функция достигает своего наибольшего и наименьшего значений всегда на границе области. Более того, можно доказать, что эти значения достигаются в точках, координаты которых имеют вид  (1 ± d). Таких точек 2
(1 ± d). Таких точек 2  = 512. В каждой из них следует вычислить определитель, а затем выбрать из полученных значений самое большое и самое маленькое. Это и будут числа M и m.
= 512. В каждой из них следует вычислить определитель, а затем выбрать из полученных значений самое большое и самое маленькое. Это и будут числа M и m.
ЛИТЕРАТУРА
1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высшая школа, 1994.
Вопросы и задачи
к защите лабораторной работы “Теория погрешностей и машинная арифметика”
1. Источники и классификация погрешностей. Приближенные числа. Абсолютная и относительная погрешности. Верные и значащие цифры. Способы округления.
2. Представление чисел в ЭВМ. Машинный нуль, машинная бесконечность, машинное эпсилон. Алгоритмы вычисления.
3. Погрешности арифметических операций над приближенными числами.
4. Погрешность вычисления функций одной и нескольких переменных.
5. Погрешность вычисления неявной функции.
6. Числа  заданы приближенно:
заданы приближенно:
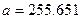 ,
,  ,
, 

 ,
,  ,
,
 ,
,  .
.
Записать эти числа со всеми верными знаками.
7. Приближенное число a содержит 5 верных цифр. Что можно сказать об относительной погрешности числа a?
8. С какой относительной погрешностью нужно найти приближенное значение числа a, чтобы верными оказались 5 значащих цифр?
9. Для приближенных чисел a и b (a > b >0) известно, что  (a)=
(a)=  (b)=
(b)=  . Оценить погрешности:
. Оценить погрешности:
а)  (a+b), b)
(a+b), b)  (a-b), c)
(a-b), c)  (a*b), d)
(a*b), d)  (a/b).
(a/b).
10. Числа  заданы приближенно:
заданы приближенно:  ,
,  ,
,  . Оценить погрешности:
. Оценить погрешности:
a) разности 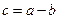 , b) произведения
, b) произведения 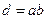 .
.
Записать ответ с учетом верных цифр.
11. Указать правила оценки абсолютных и относительных погрешностей функций
a)  , b)
, b)  , c)
, c)  .
.
12. Функция  вычисляется при значениях
вычисляется при значениях  ,
,  ,
,
 . Найти значения
. Найти значения 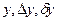 . Записать результат со всеми верными цифрами.
. Записать результат со всеми верными цифрами.
13. Коэффициенты  вычисляются с относительной погрешностью
вычисляются с относительной погрешностью  (a)=
(a)=  (b)=
(b)=  (с)=
(с)=  . Найти максимальную погрешность, с которой могут вычисляться корни уравнений:
. Найти максимальную погрешность, с которой могут вычисляться корни уравнений:
a)  , b)
, b)  .
.
14. Функция  вычисляется при значениях
вычисляется при значениях  . Определить при каких значениях
. Определить при каких значениях  ответ будет содержать 3 верные цифры.
ответ будет содержать 3 верные цифры.
15. Корни уравнения  нужно получить с четырьмя верными цифрами. С каким числом верных цифр нужно взять свободный член уравнения?
нужно получить с четырьмя верными цифрами. С каким числом верных цифр нужно взять свободный член уравнения?
Литература
1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. “Вычислительные методы для инженеров”. М.: Высшая школа, 1994.
2. Бахвалов Н.С., Лапин А.В., Чижонков Е.В. “Численные методы в задачах и упражнениях”. М.: Высшая школа, 2000.
3. Сборник задач по методам вычислений. Под ред. Монастырного П.И.. М.: Физматлит, 1994.

 . Тогда каждый элемент матрицы
. Тогда каждый элемент матрицы  = 512. В каждой из них следует вычислить определитель, а затем выбрать из полученных значений самое большое и самое маленькое. Это и будут числа M и m.
= 512. В каждой из них следует вычислить определитель, а затем выбрать из полученных значений самое большое и самое маленькое. Это и будут числа M и m. заданы приближенно:
заданы приближенно: 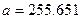 ,
,  ,
, 
 ,
,  ,
, ,
,  .
.  (a)=
(a)=  заданы приближенно:
заданы приближенно:  ,
,  ,
,  . Оценить погрешности:
. Оценить погрешности: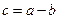 , b) произведения
, b) произведения 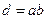 .
.  , b)
, b)  , c)
, c)  .
. вычисляется при значениях
вычисляется при значениях  ,
,  ,
, . Найти значения
. Найти значения 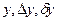 . Записать результат со всеми верными цифрами.
. Записать результат со всеми верными цифрами. , b)
, b)  .
. вычисляется при значениях
вычисляется при значениях  . Определить при каких значениях
. Определить при каких значениях  ответ будет содержать 3 верные цифры.
ответ будет содержать 3 верные цифры. нужно получить с четырьмя верными цифрами. С каким числом верных цифр нужно взять свободный член уравнения?
нужно получить с четырьмя верными цифрами. С каким числом верных цифр нужно взять свободный член уравнения?


