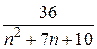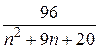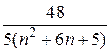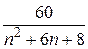ЛАБОРАТОРНАЯ РАБОТА 2.
ТЕОРИЯ ПОГРЕШНОСТЕЙ И МАШИННАЯ AРИФМЕТИКА
Мета: закріплення теоретичних знань; набуття практичних навичок обчислення у роботі В MATHCAD
Робоче місце: учбове місце в кабінеті (комп’ютерний клас)
Тривалість заняття: 90 хв.
Метеріально-технічне оснащення: методичні вказівки, комп’ютер
Хід роботи
Теоретический материал к данной теме содержится в [1, глава 2]. Варианты к задачам 1.1-1.10 даны в ПРИЛОЖЕНИИ 1.A.
Пример оформления отчета по лабораторной работе приведен в ПРИЛОЖЕНИИ 1.B.
Задача 1.1. Дан ряд  . Найти сумму ряда аналитически. Вычислить значения частичных сумм ряда . Найти сумму ряда аналитически. Вычислить значения частичных сумм ряда  и найти величину погрешности при значениях и найти величину погрешности при значениях  = = 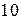 , ,  , ,  , ,  , ,  . .
ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:
1. Найти сумму ряда S аналитически как предел частичных сумм ряда (см. ПРИЛОЖЕНИЕ 1.B).
2. Используя функцию  ( ( )= )=  , вычислить значения частичных сумм , вычислить значения частичных сумм
ряда при указанных значениях  . .
3. Для каждого  вычислить величину абсолютной погрешности вычислить величину абсолютной погрешности
 и определить количество верных цифр в и определить количество верных цифр в  . .
4. Представить результаты в виде гистограммы.
Задача 1.2. Дана матрица A = 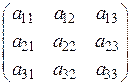 . В каждый из диагональных элементов матрицы A по очереди внести погрешность в 1%. Как изменился определитель матрицы А? Указать количество верных цифр и вычислить величину относительной погрешности определителя в каждом случае. . В каждый из диагональных элементов матрицы A по очереди внести погрешность в 1%. Как изменился определитель матрицы А? Указать количество верных цифр и вычислить величину относительной погрешности определителя в каждом случае.
Задача 1.3. Для заданной матрицы A найти обратную матрицу (если это возможно). Затем в элемент  внести погрешность в 10% и снова найти обратную матрицу. Объяснить полученные результаты. внести погрешность в 10% и снова найти обратную матрицу. Объяснить полученные результаты.
Задача 1.4. Найти ранг заданной матрицы A. Затем внести погрешность в 0.1% а) в элемент  ; b) во все элементы матрицы и снова найти ранг. Объяснить полученные результаты. ; b) во все элементы матрицы и снова найти ранг. Объяснить полученные результаты.
Задача 1.5. Дано квадратное уравнение  . Предполагается, что один из коэффициентов уравнения (в индивидуальном варианте помечен *) получен в результате округления. Произвести теоретическую оценку погрешностей корней в зависимости от погрешности коэффициента. Вычислить корни уравнения при нескольких различных значениях коэффициента в пределах заданной точности. Сравнить полученные результаты. . Предполагается, что один из коэффициентов уравнения (в индивидуальном варианте помечен *) получен в результате округления. Произвести теоретическую оценку погрешностей корней в зависимости от погрешности коэффициента. Вычислить корни уравнения при нескольких различных значениях коэффициента в пределах заданной точности. Сравнить полученные результаты.
Задача 1.6. Для пакета MATHCAD найти значения машинного нуля, машинной бесконечности, машинного эпсилон (см. ПРИЛОЖЕНИЕ 1.B).
Задача 1.7. Вычислить значения машинного нуля, машинной бесконечности, машинного эпсилон в режимах одинарной, двойной и расширенной точности на двух алгоритмических языках. Сравнить результаты.
Задача 1.8. Составить программу, моделирующую вычисления на ЭВМ с ограниченной разрядностью m. Решить задачу 1.1 для случая  =10000, используя эту программу. Составить график зависимости погрешности от количества разрядов m =4,5,…8. =10000, используя эту программу. Составить график зависимости погрешности от количества разрядов m =4,5,…8.
Задача 1.9. Для матрицы A решить вопрос о существовании обратной матрицы в следующих случаях:
1) элементы матрицы заданы точно;
2) элементы матрицы заданы приближенно с относительной погрешностью a)  =a% и b) =a% и b)  = b%. Найти относительную погрешность результата. = b%. Найти относительную погрешность результата.
УКАЗАНИЕ. См. ПРИЛОЖЕНИЕ 1.С.
Задача 1.10. Три вектора  , ,  , , 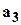 заданы своими координатами в базисе i, j, k. Что можно сказать о компланарности этих векторов, если: 1) координаты векторов заданы точно; заданы своими координатами в базисе i, j, k. Что можно сказать о компланарности этих векторов, если: 1) координаты векторов заданы точно;
2) координаты векторов заданы приближённо с относительной погрешностью а) d = a %; б) d = b %.
УКАЗАНИЕ. См. ПРИЛОЖЕНИЕ 1.С.
ПРИЛОЖЕНИЕ 1.A.
Cхема вариантов к лабораторной работе 1
| N
| Выполняемые задачи
| N
| Выполняемые задачи
| |
| 1.1.1, 1.2.1, 1.7, 1.6, 1.10.1
|
| 1.1.16, 1.5.4, 1.7, 1.6, 1.8
| |
| 1.1.2, 1.3.1, 1,7, 1.6, 1.10.2
|
| 1.1.17, 1.2.5, 1.7, 1.6, 1.8
| |
| 1.1.3, 1.4.1, 1.7, 1.6, 1.10.3
|
| 1.1.18, 1.3.5, 1.7, 1.6, 1.8
| |
| 1.1.4, 1.5.1, 1.7, 1.6, 1.10.4
|
| 1.1.19, 1.4.5, 1.7, 1.6, 1.9.1
| |
| 1.1.5, 1.2.2, 1.7, 1.6, 1.10.5
|
| 1.1.20, 1.5.5, 1.7, 1.6, 1.9.2
| |
| 1.1.6, 1.3.2, 1.7, 1.6, 1.10.6
|
| 1.1.21, 1.2.6, 1.7, 1.6, 1.9.3
| |
| 1.1.7, 1.4.2, 1.7, 1.6, 1.9.1
|
| 1.1.22, 1.3.6, 1.7, 1.6, 1.9.4
| |
| 1.1.8, 1.5.2, 1.7, 1.6, 1.9.2
|
| 1.1.23, 1.4.6, 1.7, 1.6, 1.9.5
| |
| 1.1.9, 1.2.3, 1.7, 1.6, 1.9.3
|
| 1.1.24, 1.5.6, 1.7, 1.6, 1.9.6
| |
| 1.1.10, 1.3.3, 1.7, 1.6, 1.9.4
|
| 1.1.25, 1.2.1, 1.7, 1.6, 1.10.1
| |
| 1.1.11, 1.4.3, 1.7, 1.6, 1.9.5
|
| 1.1.26, 1.3.1, 1.7, 1.6, 1.10.2
| |
| 1.1.12, 1.5.3, 1.7, 1.6, 1.8
|
| 1.1.27, 1.4.1, 1.7, 1.6, 1.10.3
| |
| 1.1.13, 1.2.4, 1.7, 1.6, 1.8
|
| 1.1.28, 1.5.1, 1.7, 1.6, 1.10.4
| |
| 1.1.14, 1.3.4, 1.7, 1.6, 1.8
|
| 1.1.29, 1.2.2, 1.7, 1.6, 1.10.5
| |
| 1.1.15, 1.4.4, 1.7, 1.6, 1.8
|
| 1.1.30, 1.3.2, 1.7, 1.6, 1.10.6
|
ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 1
Таблица к задаче 1.1
| N
| 
| N
| 
| N
| 
| | 1.1.1
| 
| 1.1.11
| 
| 1.1 21
| 
| | 1.1.2
| 
| 1.1.12
| 
| 1.1.22
| 
| | 1.1.3
| 
| 1.1.13
| 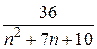
| 1.1.23
| 
| | 1.1.4
| 
| 1.1.14
| 
| 1.1.24
| 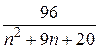
| | 1.1.5
| 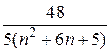
| 1.1.15
|  
| 1.1.25
| 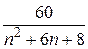
| | 1.1.6
| 
| 1.1.16
| 
| 1.1.26
| 
| | 1.1.7
| 
| 1.1.17
| 
| 1.1.27
| 
| | 1.1.8
| 
| 1.1.18
| 
| 1.1.28
| 
| | 1.1.9
| 
| 1.1.19
| 
| 1.1.29 
| 
| | 1.1.10
| 
| 1.1.20
| 
| 1.1.30
| 
| Таблица к задаче 1.2
| N
| A
| N
| A
| N
| A
| | 1.2.1
| 3 2 2
33 28 24
360 320 270
| 1.2.2
| 30 34 19
314 354 200
2 8 13
| 1.2.3
| 1.3 1 13
3.4 1.4 23
5 3 1.5
| | 1.2.4
| 9 5 6
17 9 11
7 4 5
| 1.2.5
| -7 -7 -1
0 -2 -6
5 6 4
| 1.2.6
| 3 1 13
5 3 15
11 5 40
| Таблица к задаче 1.3
| N
| A
| N
| A
| N
| A
| | 1.3.1
| 2 16 -6
3 24 5
1 8 11
| 1.3.2
| 2 4.4 -2
1 2 -1
3 -5 0
| 1.3.3
| 3 5 3
9 15 9
6 7 2
| | 1.3.4
| 48 3 6
32 2 4
5 -1 2
| 1.3.5
| 2 0.4 6
1.1 0.2 3
2.3 1.2 4
| 1.3.6
| 5 5.5 5.5
1 1 1
5 -1 2
| Таблица к задаче 1.4
| N
| A
| N
| A
| N
| A
| | 1.4.1
| 1.1 0.1 0.8 1.6
1.3 -0.3 1.2 2.1
0.9 0.5 0.4 1.1
-0.4 -3.8 2 1.3
| 1.4.2
| 0.6 4.5 0.3 3
-2.4 -12 0.9 -7
1.2 9 0.6 6
-1.2 3 3.6 4
| 1.4.3
| 1.8 4 0 1.9
20.9 37 -25 19.2
0.5 3 5 1.1
10.6 16 -20 8.9
| | 1.4.4
| 2 15 22 7
1 14.1 18.8 2.3
2 4 9 9
-0.4 2.5 2.1 -2.4
| 1.4.5
| 1.9 9 1.6 0.1
11.3 23 6.8 -3.7
0.5 10 1.1 1.1
0.9 -11 -0.6 -2.1
| 1.4.6
| 1.2 9 0.6 6
1.6 23 -7.2 9
2 4 9 9
2 37 -15 12
|
Таблица к задаче 1.5
| N
| Коэффициенты
| N
| Коэффициенты
| N
| Коэффициенты
| | 1.5.1
| b* = -39.6
c = -716.85
| 1.5.2
| b = 27.4
 c* = 187.65 c* = 187.65
| 1.5.3
| b* = 37.4
c = 187.65
| | 1.5.4
| b = -30.9
c* = 238.7
| 1.5.5
| b* = -3.29
c = 2.706
| 1.5.6
| b = -3.29
c* = 2.706
|
Таблица к задаче 1.9
| N
| A
| a
| b
| N
| A
| a
| b
| | 1.9.1
| 31 27 22
32.2 28.2 24
36 32 27
|
0.1
|
0.4
| 1.9.2
| 30 34 19
31.4 35.4 20
24 28 13
|
0.05
|
0.1
| | 1.9.3
| 3 1 13
13.4 11.4 23
5 3 15
|
0.05
|
0.1
| 1.9.4
| 9 5 6
13.5 9.5 11
8 4 5
|
0.1
|
0.5
| | 1.9.5
| -7 -8 -10
28.6 27.6 25
7 6 4
|
0.1
|
0.2
| 1.9.6
| -3 -1 -13
26.8 22.4 46
5 3 15
|
0.1
|
0.1
|
Таблица к задаче 1.10
| N
| а1
| а2
| а3
| a
| b
| | 1.10.1
| (10, 15, 1)
| (0.7, 5.7, -9)
| (11, 16, 2)
| 0.05
| 0.1
| | 1.10.2
| (- 2, - 5, 13)
| (14.2, 11.2, 28)
| (0, -3, 15)
| 0.5
| 0.1
| | 1.10.3
| (24, 28, 13)
| (21.1, 25.1, 10)
| (18, 22, 7)
| 0.05
| 0.01
| | 1.10.4
| (9, 17, 1)
| (27, 35, -18)
| (6, 14, 4)
| 0.5
| 0.1
| | 1.10.5
| (14, 4, 17)
| (33.9, 23.9, 38)
| (13, 3, 16)
| 0.05
| 0.1
| | 1.10.6
| (9, 17, 1)
| (27, 35, -18)
| (6, 14, 4)
| 0.5
| 0.1
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
ИГРЫ НА ТАКТИЛЬНОЕ ВЗАИМОДЕЙСТВИЕ Методические рекомендации по проведению игр на тактильное взаимодействие...
Реформы П.А.Столыпина Сегодня уже никто не сомневается в том, что экономическая политика П...
Виды нарушений опорно-двигательного аппарата у детей В общеупотребительном значении нарушение опорно-двигательного аппарата (ОДА) идентифицируется с нарушениями двигательных функций и определенными органическими поражениями (дефектами)...
|
ТЕХНИКА ПОСЕВА, МЕТОДЫ ВЫДЕЛЕНИЯ ЧИСТЫХ КУЛЬТУР И КУЛЬТУРАЛЬНЫЕ СВОЙСТВА МИКРООРГАНИЗМОВ. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА БАКТЕРИЙ Цель занятия. Освоить технику посева микроорганизмов на плотные и жидкие питательные среды и методы выделения чистых бактериальных культур. Ознакомить студентов с основными культуральными характеристиками микроорганизмов и методами определения...
САНИТАРНО-МИКРОБИОЛОГИЧЕСКОЕ ИССЛЕДОВАНИЕ ВОДЫ, ВОЗДУХА И ПОЧВЫ Цель занятия.Ознакомить студентов с основными методами и показателями...
Меры безопасности при обращении с оружием и боеприпасами 64. Получение (сдача) оружия и боеприпасов для проведения стрельб осуществляется в установленном порядке[1].
65. Безопасность при проведении стрельб обеспечивается...
|
|

 . Найти сумму ряда аналитически. Вычислить значения частичных сумм ряда
. Найти сумму ряда аналитически. Вычислить значения частичных сумм ряда  и найти величину погрешности при значениях
и найти величину погрешности при значениях  =
= 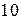 ,
,  ,
,  ,
,  ,
,  .
. (
( , вычислить значения частичных сумм
, вычислить значения частичных сумм и определить количество верных цифр в
и определить количество верных цифр в  .
.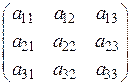 . В каждый из диагональных элементов матрицы A по очереди внести погрешность в 1%. Как изменился определитель матрицы А? Указать количество верных цифр и вычислить величину относительной погрешности определителя в каждом случае.
. В каждый из диагональных элементов матрицы A по очереди внести погрешность в 1%. Как изменился определитель матрицы А? Указать количество верных цифр и вычислить величину относительной погрешности определителя в каждом случае. внести погрешность в 10% и снова найти обратную матрицу. Объяснить полученные результаты.
внести погрешность в 10% и снова найти обратную матрицу. Объяснить полученные результаты. . Предполагается, что один из коэффициентов уравнения (в индивидуальном варианте помечен *) получен в результате округления. Произвести теоретическую оценку погрешностей корней в зависимости от погрешности коэффициента. Вычислить корни уравнения при нескольких различных значениях коэффициента в пределах заданной точности. Сравнить полученные результаты.
. Предполагается, что один из коэффициентов уравнения (в индивидуальном варианте помечен *) получен в результате округления. Произвести теоретическую оценку погрешностей корней в зависимости от погрешности коэффициента. Вычислить корни уравнения при нескольких различных значениях коэффициента в пределах заданной точности. Сравнить полученные результаты. =a% и b)
=a% и b)  ,
,  ,
, 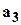 заданы своими координатами в базисе i, j, k. Что можно сказать о компланарности этих векторов, если: 1) координаты векторов заданы точно;
заданы своими координатами в базисе i, j, k. Что можно сказать о компланарности этих векторов, если: 1) координаты векторов заданы точно;