Задание 2. Решить систему (2.1) методом простой итерации
Решить систему (2.1) методом простой итерации. Предполагается в дальнейшем, что матрица А квадратная и невырожденная. Предварительно приведем систему (2.2) к итерационному виду:
Для произвольного начального вектора
сходится, если выполнено одно из условий [2] а) б) в) Процесс вычислений заканчиваем при выполнении условия
где Задание 3 Решить систему (2.1) методом Зейделя. Метод Зейделя отличается от метода простой итерации тем, что найдя какое-то значение для компоненты, мы на следующем шаге используем его для отыскания следующей компоненты. Вычисления ведутся по формуле
Каждое из условий (2.4)-(2.6) является достаточным для сходимости итерационного процесса по методу Зейделя. Практически же удобнее следующее преобразование системы (2.2). Домножая обе части (2.2) на АТ, получим эквивалентную ей систему
где Примерный вариант выполнения лабораторной работы
Пример. Решите систему уравнений X1+2X2+3X3=7, X1-3X2+2X3=5, X1+X2+X3=3.
|

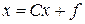 (2.3)
(2.3)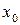 итерационный процесс
итерационный процесс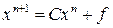
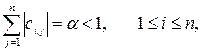 (2.4)
(2.4)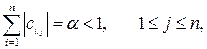 (2.5)
(2.5)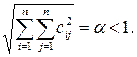 (2.6)
(2.6)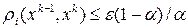 (2.7)
(2.7)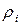 (i=1,2,3)- одна из метрик, определяемая левой частью (2.4)-(2.6), по которой была установлена сходимость,
(i=1,2,3)- одна из метрик, определяемая левой частью (2.4)-(2.6), по которой была установлена сходимость, 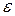 - заданная точность (
- заданная точность (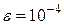 ).
). (2.8)
(2.8)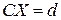 ,
,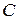 =
= 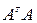 и d =
и d = 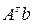 . Далее, поделив каждое уравнение на
. Далее, поделив каждое уравнение на 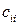 , приведем систему к виду (2.8). Подобное преобразование также гарантирует сходимость итерационного процесса.
, приведем систему к виду (2.8). Подобное преобразование также гарантирует сходимость итерационного процесса.


