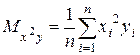Найти оценки для параметров модели y =b0 + b1 x + b2 x 2.
1.
| x
| 0.5
| 1.0
| 1.5
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
|
| y
| 0.4
| 0.3
| 1.0
| 1.7
| 2.1
| 3.4
| 4.1
| 5.8
|
2.
| x
| 4.5
| 5.0
| 5.5
| 6.0
| 6.5
| 7.0
| 7.5
| 8.0
|
| y
| 7.7
| 9.4
| 11.4
| 13.6
| 15.6
| 18.6
| 21.2
| 24.1
|
3.
| x
| 0.4
| 0.8
| 1.2
| 1.6
| 2.0
| 2.4
| 2.8
| 3.2
| 3.6
|
| y
| 0.43
| 0.94
| 1.91
| 3.01
| 4.0
| 4.56
| 6.45
| 8.59
| 11.15
|
4.
| x
| 4.0
| 4.4
| 4.8
| 5.2
| 5.6
| 6.0
| 6.4
| 6.8
|
| y
| 13.88
| 16.93
| 20.47
| 24.15
| 28.29
| 32.61
| 37.41
| 42.39
|
Найти оценки для параметров модели y =b0 + b1 x.
5.
| x
|
|
|
|
|
|
|
| y
| 2.11
| 2.45
| 2.61
| 2.73
| 2.75
| 2.81
|
6.
| x
| 0.3
| 0.6
| 0.9
| 1.2
| 1.5
| 1.8
|
| y
| 4.39
| 4.75
| 4.98
| 5.11
| 5.12
| 5.18
|
Найти оценки для параметров модели y =b0 + b1 exp (0.1 x).
7.
| x
|
|
|
|
|
|
|
| y
| 0.1
| 0.21
| 0.43
| 0.51
| 0.62
| 0.81
|
8.
| x
| 1.0
| 1.5
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
|
| y
| 4.11
| 4.16
| 4.23
| 4.29
| 4.36
| 4.42
| 4.53
|
Найти оценки для параметров модели y =b0 + b1 sinx + b2 cosx.
9.
| x
| 0.5
| 1.0
| 1.5
| 2.0
| 2.5
| 3.0
| 3.5
| 4.0
|
| y
| 2.47
| 2.86
| 3.01
| 2.91
| 2.55
| 2.11
| 2.61
| 1.25
|
Пусть зависимость между переменными  и
и 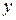 задана таблично (заданы опытные данные). Требуется найти функцию в некотором смысле наилучшим образом описывающую данные. Одним из способов подбора такой (приближающей) функции является метод наименьших квадратов. Метод состоит в том, чтобы сумма квадратов отклонений значений искомой функции
задана таблично (заданы опытные данные). Требуется найти функцию в некотором смысле наилучшим образом описывающую данные. Одним из способов подбора такой (приближающей) функции является метод наименьших квадратов. Метод состоит в том, чтобы сумма квадратов отклонений значений искомой функции  и заданной таблично
и заданной таблично  была наименьшей:
была наименьшей:
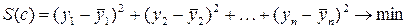 (6.1)
(6.1)
где  - вектор параметров искомой функции.
- вектор параметров искомой функции.
Задание 2
Построить методом наименьших квадратов две эмпирические формулы: линейную и квадратичную.
В случае линейной функции  задача сводится нахождению параметров
задача сводится нахождению параметров  и
и  из системы линейных уравнений
из системы линейных уравнений
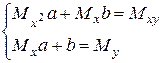 , где
, где
 ,
, 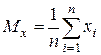 ,
,  , My=
, My= 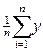 i
i
а в случае квадратичной зависимости  к нахождению параметров
к нахождению параметров  ,
,  и
и  из системы уравнений:
из системы уравнений:
 , где
, где
 ,
, 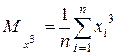 ,
, 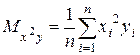
Выбрать из двух функций наиболее подходящую. Для этого составить таблицу для подсчета суммы квадратов уклонений по формуле (6. 1 ). Исходные данные взять из таблицы 6.

 и
и 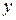 задана таблично (заданы опытные данные). Требуется найти функцию в некотором смысле наилучшим образом описывающую данные. Одним из способов подбора такой (приближающей) функции является метод наименьших квадратов. Метод состоит в том, чтобы сумма квадратов отклонений значений искомой функции
задана таблично (заданы опытные данные). Требуется найти функцию в некотором смысле наилучшим образом описывающую данные. Одним из способов подбора такой (приближающей) функции является метод наименьших квадратов. Метод состоит в том, чтобы сумма квадратов отклонений значений искомой функции  и заданной таблично
и заданной таблично  была наименьшей:
была наименьшей: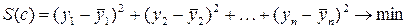 (6.1)
(6.1) - вектор параметров искомой функции.
- вектор параметров искомой функции. задача сводится нахождению параметров
задача сводится нахождению параметров  и
и  из системы линейных уравнений
из системы линейных уравнений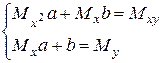 , где
, где ,
, 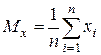 ,
,  , My=
, My= 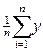 i
i к нахождению параметров
к нахождению параметров  ,
,  и
и  , где
, где ,
, 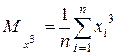 ,
,