Стандартная система
Чтобы не «привязываться» к конкретной структурной схеме, программы для проектирования оптимальных регуляторов обычно используют так называемую стандартную систему, где выделяют 4 типа сигналов и связанных с ними передаточных функций:
Уравнения системы (в изображениях по Лапласу) можно записать так:
Справа показано общепринятое обозначение стандартной системы. Обратите внимание, что в ней (формально) используется положительная обратная связь. При построении передаточных функций Каждый из четырех сигналов может быть векторным, то есть, содержать несколько компонент. Например, в рассмотренной выше задаче стабилизации судна на курсе требовалось ограничить сумму дисперсий Здесь Построим стандартную систему для задачи оптимальной стабилизации судна на курсе, которая рассматривалась выше. Здесь добавлен фильтр
Вектор внешних воздействий в задаче оптимизации при случайных возмущениях должен описываться моделью единичного белого шума. В данном случае он состоит из двух компонент, независимых сигналов
Поэтому
Обратите внимание, что отрицательная обратная связь здесь выражается в том, что в записи
|

 – сигнал ошибки, его нужно сделать «минимальным»;
– сигнал ошибки, его нужно сделать «минимальным»; – измеренный сигнал обратной связи, поступающий на вход регулятора;
– измеренный сигнал обратной связи, поступающий на вход регулятора;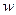 – внешнее возмущение;
– внешнее возмущение;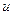 – управляющий сигнал на выходе регулятора.
– управляющий сигнал на выходе регулятора.

 предполагается, что регулятора в контуре нет (цепь разорвана).
предполагается, что регулятора в контуре нет (цепь разорвана). . Ее можно представить как дисперсию векторного сигнала
. Ее можно представить как дисперсию векторного сигнала  , которая по определению равна:
, которая по определению равна: 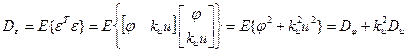 .
. обозначает математическое ожидание выражения в фигурных скобках, верхний индекс
обозначает математическое ожидание выражения в фигурных скобках, верхний индекс 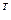 – операцию транспонирования. Также учитывается, что сигналы центрированные, поэтому математическое ожидание квадрата сигнала равно его дисперсии.
– операцию транспонирования. Также учитывается, что сигналы центрированные, поэтому математическое ожидание квадрата сигнала равно его дисперсии. , который формирует спектр помехи измерений. Его входной сигнал
, который формирует спектр помехи измерений. Его входной сигнал  описывается как единичный белый шум, независимый от
описывается как единичный белый шум, независимый от 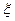 .
.

 ,
,  ,
,  ,
,  .
. появляется знак «минус». Можно показать, что
появляется знак «минус». Можно показать, что 


