Анализ случайных процессов в Matlab
Чтобы вычислить дисперсию и СКВО случайного процесса, значения которого записаны в массив x, применяются функции var и std: v = var(x); % дисперсия sigma = std(x); % среднеквадратическое отклонение
R = xcorr(x) / length(x); Если построить ее мы получим значения как для положительных, так и для отрицательных Rplus = R(floor(length(R)/2):end); Здесь функция length вычисляет длину массива, а floor – округляет результат в меньшую сторону. Для оценки спектра в заданном частотном диапазоне, например,
Sw = []; for i=1:length(w) Sw(i) = sum(Rplus.* cos(w(i)*t)); end; Sw = 2*T*Sw; Здесь в массиве t записано время, соответствующее отсчетам оценки корреляционной функции Rplus для положительных При использовании окна нужно предварительно умножить корреляционную функцию на весовые коэффициенты. Например, для окна Хэмминга hamm = 0.54 + 0.46*cos(pi*t/max(t)); Rplus = Rplus.* hamm; Потом выполняется программа оценки спектра, приведенная выше. Второй метод использует дискретное преобразование Фурье для исходного сигнала. N = 512; % число точек (степень двойки) w = 2*pi*[0:N/2] / N / T; % сетка угловых частот Fw = T * fft(x, N); % оценка F_X(w) Sw = Fw.* conj(Fw) / N / T; % оценка S_X(w) Sw = Sw(1:N/2+1); % взяли первую половину
|

 Для анализа корреляционной функции удобно использовать функции пакета Signal Processing Toolbox (обработка сигналов). Функция xcorr вычисляет двустороннюю корреляционную функцию
Для анализа корреляционной функции удобно использовать функции пакета Signal Processing Toolbox (обработка сигналов). Функция xcorr вычисляет двустороннюю корреляционную функцию 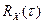 . Для того, чтобы получить правильные абсолютные значения корреляционной функции, результат нужно разделить на количество отсчетов исходного сигнала. Например, если значения сигнала находятся в массиве x, корреляционная функция может быть вычислена так:
. Для того, чтобы получить правильные абсолютные значения корреляционной функции, результат нужно разделить на количество отсчетов исходного сигнала. Например, если значения сигнала находятся в массиве x, корреляционная функция может быть вычислена так: . Если нужны только значения при
. Если нужны только значения при  , первую часть приходится «обрезать», учитывая, что график симметричный.
, первую часть приходится «обрезать», учитывая, что график симметричный.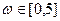 рад/с, можно использовать два подхода. Метод Блэкмана-Тьюки использует преобразование Фурье корреляционной функции:
рад/с, можно использовать два подхода. Метод Блэкмана-Тьюки использует преобразование Фурье корреляционной функции: w = [0:0.1:5];
w = [0:0.1:5];


