Расчет оптимального регулятора для замкнутых систем (систем управления с обратной связью) выполняется почти так же, как и синтез оптимальных фильтров. Однако нужно учитывать две особенности:
1) регулятор должен обеспечивать устойчивость замкнутой системы (в задаче фильтрации требовалась устойчивость самого фильтра);
2) уменьшение дисперсии ошибки, как правило, достигается за счет увеличения мощности управления, которая ограничена в реальных задачах; например, угол перекладки руля судна не может быть больше 30-35°.
Рассмотрим систему стабилизации судна на курсе в условиях морского волнения.

Модель судна (обведена штриховой линией) состоит из двух блоков с передаточными функциями  и
и  (интегрирующее звено). Истинный курс
(интегрирующее звено). Истинный курс 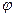 измеряется датчиком с передаточной функцией
измеряется датчиком с передаточной функцией  . Для компенсации измеренной ошибки
. Для компенсации измеренной ошибки  регулятор
регулятор  выдает на привод (с передаточной функцией
выдает на привод (с передаточной функцией 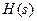 ) управляющий сигнал
) управляющий сигнал 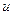 , который преобразуется в угол поворота руля
, который преобразуется в угол поворота руля  . Заметим, что сама ошибка не измеряется, вместо нее регулятор получает сигнал
. Заметим, что сама ошибка не измеряется, вместо нее регулятор получает сигнал  , который можно назвать оценкой ошибки.
, который можно назвать оценкой ошибки.
На систему действуют два случайных сигнала: возмущение 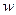 , вызванное морским волнением и имеющее спектральную плотность
, вызванное морским волнением и имеющее спектральную плотность  , и белый шум измерений
, и белый шум измерений 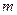 . Для моделирования возмущения используется формирующий фильтр
. Для моделирования возмущения используется формирующий фильтр  (такой, что
(такой, что 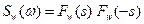 ), на вход которого поступает белый шум с единичной интенсивностью. Далее мы будем считать, что
), на вход которого поступает белый шум с единичной интенсивностью. Далее мы будем считать, что  и все случайные сигналы – центрированные.
и все случайные сигналы – центрированные.
Какова же цель управления? Очевидно, что нужно сделать минимальной дисперсию 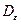 ошибки
ошибки  (при
(при  ). Это может быть обеспечено только с помощью управления, то есть, за счет увеличения активности руля. В то же время, постоянные «дергания» руля крайне нежелательны, поэтому нужно ограничить дисперсию
). Это может быть обеспечено только с помощью управления, то есть, за счет увеличения активности руля. В то же время, постоянные «дергания» руля крайне нежелательны, поэтому нужно ограничить дисперсию  (мощность) сигнала управления
(мощность) сигнала управления 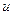 . Задача оптимизации состоит в том, чтобы выбрать передаточную функцию регулятора
. Задача оптимизации состоит в том, чтобы выбрать передаточную функцию регулятора  так, чтобы
так, чтобы
 .
.
(6)
Если не ограничивать управление, то есть принять  , мощность управления практически всегда будет неограниченно расти, что неприемлемо.
, мощность управления практически всегда будет неограниченно расти, что неприемлемо.
Вычисление дисперсий ошибки и управления выполним через их спектральные плотности. Для простоты пока не будем учитывать шум измерений. Тогда
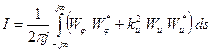 ,
,
где  и
и  – передаточные функции от входа
– передаточные функции от входа 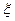 (белого шума) к углу рыскания
(белого шума) к углу рыскания 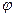 и сигналу управления
и сигналу управления 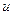 . Используя правила преобразования структурных схем, находим
. Используя правила преобразования структурных схем, находим
 ,
,  .
.
где  . Здесь от выбора регулятора
. Здесь от выбора регулятора  зависит только функция
зависит только функция
 ,
,
(7)
поэтому спектральные плотности угла рыскания и управления можно вычислить как
 ,
,  .
.
После простых преобразований, критерий качества (6) можно записать в виде Ошибка! Источник ссылки не найден., где
 ,
,
(8)
то есть, подынтегральное выражение имеет вид Ошибка! Источник ссылки не найден., где вместо  фигурирует
фигурирует  , а функции
, а функции  ,
,  и
и  известны (конечно, они отличаются от тех, что были в задаче фильтрации). При этом сразу возникает вопрос: нельзя ли использовать здесь тот же способ оптимизации, который применяется для построения фильтра Винера?
известны (конечно, они отличаются от тех, что были в задаче фильтрации). При этом сразу возникает вопрос: нельзя ли использовать здесь тот же способ оптимизации, который применяется для построения фильтра Винера?
Несложно показано, что  – это в самом деле передаточная функция замкнутой системы от
– это в самом деле передаточная функция замкнутой системы от  к
к 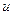 , то есть, для устойчивости системы она должна быть устойчива, как и фильтр Винера. Тогда можно было бы сначала найти оптимальную устойчивую функцию
, то есть, для устойчивости системы она должна быть устойчива, как и фильтр Винера. Тогда можно было бы сначала найти оптимальную устойчивую функцию  как оптимальный фильтр Винера, а затем выразить передаточную функцию регулятора
как оптимальный фильтр Винера, а затем выразить передаточную функцию регулятора  из (7). Однако такой метод «проходит» только тогда, когда сам объект устойчив. В общем случае (если объект может быть неустойчивым) приходится использовать различные «хитрости», чтобы свести задачу оптимизации замкнутой системы к задаче Винера и при этом гарантировать устойчивость системы.
из (7). Однако такой метод «проходит» только тогда, когда сам объект устойчив. В общем случае (если объект может быть неустойчивым) приходится использовать различные «хитрости», чтобы свести задачу оптимизации замкнутой системы к задаче Винера и при этом гарантировать устойчивость системы.
Современный подход основан на использовании параметризации всех стабилизирующих регуляторов. Так называется выражение для передаточной функции регулятора, которое зависит от неизвестной устойчивой функции. Изменяя эту функции произвольным образом (но сохраняя ее устойчивость) мы можем получить любой регулятор, который стабилизирует систему. С другой стороны, в такой форме можно представить любой регулятор, который стабилизирует систему.
Для построения параметризации передаточную функцию разомкнутого контура (без регулятора) представляют в виде отношения полиномов, 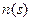 и
и  :
:
 .
.
(9)
Если полиномы 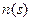 и
и  не имеют общих корней, то существуют полиномы
не имеют общих корней, то существуют полиномы 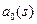 и
и  , удовлетворяющие уравнению
, удовлетворяющие уравнению  .
.
(10)
Это полиномиальное уравнение, то есть уравнение, в котором неизвестными являются полиномы (многочлены). Степени полиномов 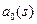 и
и  на единицу меньше, чем степени
на единицу меньше, чем степени  и
и 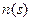 соответственно. Приравнивание коэффициентов при одинаковых степенях
соответственно. Приравнивание коэффициентов при одинаковых степенях  в левой и правой частях уравнения дает линейную систему уравнений, которая легко решается современными программными средствами.
в левой и правой частях уравнения дает линейную систему уравнений, которая легко решается современными программными средствами.
Параметризация всех стабилизирующих регуляторов имеет вид  ,
,
(11)
где 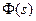 произвольная устойчивая дробно-рациональная функция (то есть, все корни ее знаменателя имеют отрицательные вещественные части). Любой регулятор, построенный по этой формуле – стабилизирующий, в то же время любой стабилизирующий регулятор может быть представлен в таком виде для некоторой функции
произвольная устойчивая дробно-рациональная функция (то есть, все корни ее знаменателя имеют отрицательные вещественные части). Любой регулятор, построенный по этой формуле – стабилизирующий, в то же время любой стабилизирующий регулятор может быть представлен в таком виде для некоторой функции 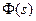 .
.
Подставляя выражение (11) для  в (7), находим, учитывая (9) и (10):
в (7), находим, учитывая (9) и (10): 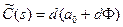 .
.
В свою очередь, подставляя это выражение в (8), получаем  ,
,
где  ,
, 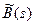 и
и  – известные функции. Поскольку любая устойчивая функция
– известные функции. Поскольку любая устойчивая функция 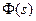 дает стабилизирующий регулятор (11), мы свели исходную задачу к задаче Винера, которую можно решать известными средствами (применяя факторизацию и сепарацию).
дает стабилизирующий регулятор (11), мы свели исходную задачу к задаче Винера, которую можно решать известными средствами (применяя факторизацию и сепарацию).


 и
и  (интегрирующее звено). Истинный курс
(интегрирующее звено). Истинный курс 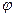 измеряется датчиком с передаточной функцией
измеряется датчиком с передаточной функцией  . Для компенсации измеренной ошибки
. Для компенсации измеренной ошибки  регулятор
регулятор  выдает на привод (с передаточной функцией
выдает на привод (с передаточной функцией 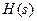 ) управляющий сигнал
) управляющий сигнал 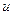 , который преобразуется в угол поворота руля
, который преобразуется в угол поворота руля  . Заметим, что сама ошибка не измеряется, вместо нее регулятор получает сигнал
. Заметим, что сама ошибка не измеряется, вместо нее регулятор получает сигнал  , который можно назвать оценкой ошибки.
, который можно назвать оценкой ошибки.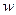 , вызванное морским волнением и имеющее спектральную плотность
, вызванное морским волнением и имеющее спектральную плотность  , и белый шум измерений
, и белый шум измерений 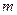 . Для моделирования возмущения используется формирующий фильтр
. Для моделирования возмущения используется формирующий фильтр  (такой, что
(такой, что 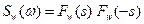 ), на вход которого поступает белый шум с единичной интенсивностью. Далее мы будем считать, что
), на вход которого поступает белый шум с единичной интенсивностью. Далее мы будем считать, что  и все случайные сигналы – центрированные.
и все случайные сигналы – центрированные.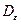 ошибки
ошибки  (при
(при  (мощность) сигнала управления
(мощность) сигнала управления  .
. , мощность управления практически всегда будет неограниченно расти, что неприемлемо.
, мощность управления практически всегда будет неограниченно расти, что неприемлемо.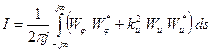 ,
, и
и  – передаточные функции от входа
– передаточные функции от входа 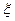 (белого шума) к углу рыскания
(белого шума) к углу рыскания  ,
,  .
. . Здесь от выбора регулятора
. Здесь от выбора регулятора  ,
, ,
,  .
. ,
, , а функции
, а функции  ,
,  и
и  известны (конечно, они отличаются от тех, что были в задаче фильтрации). При этом сразу возникает вопрос: нельзя ли использовать здесь тот же способ оптимизации, который применяется для построения фильтра Винера?
известны (конечно, они отличаются от тех, что были в задаче фильтрации). При этом сразу возникает вопрос: нельзя ли использовать здесь тот же способ оптимизации, который применяется для построения фильтра Винера?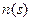 и
и  :
: .
.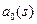 и
и  , удовлетворяющие уравнению
, удовлетворяющие уравнению  .
. в левой и правой частях уравнения дает линейную систему уравнений, которая легко решается современными программными средствами.
в левой и правой частях уравнения дает линейную систему уравнений, которая легко решается современными программными средствами. ,
,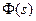 произвольная устойчивая дробно-рациональная функция (то есть, все корни ее знаменателя имеют отрицательные вещественные части). Любой регулятор, построенный по этой формуле – стабилизирующий, в то же время любой стабилизирующий регулятор может быть представлен в таком виде для некоторой функции
произвольная устойчивая дробно-рациональная функция (то есть, все корни ее знаменателя имеют отрицательные вещественные части). Любой регулятор, построенный по этой формуле – стабилизирующий, в то же время любой стабилизирующий регулятор может быть представлен в таком виде для некоторой функции 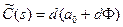 .
. ,
, ,
, 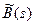 и
и  – известные функции. Поскольку любая устойчивая функция
– известные функции. Поскольку любая устойчивая функция 


