Распознавание по расстояниям в n-мерном пространстве

Эталонные изображения Х₁, X₂,...,Х_т некоторого числа т различных классов изображений или образов в n -мерном пространстве задаются в виде точек (x₁₁, x₁₂, …, x_1n), (x₂₁, x₂₂, …, x_2n),..., (x_m1, x_m2, …, x_mn). Любое входное изображение Si также представляется в виде точки (x_si1, x_si2,, …, x_sin) в этом пространстве. Принадлежность входного изображения S_k к одному из т классов определяется с помощью расстояний между точкой S_i и всеми точками Х₁, X₂,...,Х_т соответствующими эталонным образам. Расстояние и является мерой сходства входного изображения с эталонами классов или образов. Входное изображение относится к тому образу, расстояние до эталонного изображения которого минимально, т.е. решающим правилом является следующее соотношение

(1)

В теории распознавания образов часто используются расстояния по Евклиду (2) и по Минковскому (3):

(2)

(3)

где λ — целое положительное число, большее двух.

Операции возведения в степень и извлечения корня не всегда удобно использовать при определении расстояний, поскольку они являются нелинейными операциями. Поэтому для определения расстояний в пространстве изображений часто используется и сумма модулей разностей между соответствующими компонентами n -мерных векторов:

(4)

В выражения (2) - (4) разности всех компонентов векторов входят с одинаковыми единичными весами. В тех случаях, когда компоненты векторов, соответствующих распознаваемым изображениям, отличаются на порядки, например, одни компоненты векторов измеряются метрами, а другие — сантиметрами или миллиметрами, то при использовании расстояний (2) — (4) компоненты, имеющие небольшие численные значения, могут практически не влиять на величину расстояний. В то же время с точки зрения решения реальных задач распознавания именно эти компоненты могут играть определяющую роль. Поэтому для более адекватного учета подобных компонент в выражения (2) — (4) могут вводиться весовые коэффициенты, учитывающие практическую ценность различных компонент вектора. В этом случае выражения (2) — (4) преобразуются к виду:

(5)

(6)

(7)

Предварительное задание весовых коэффициентов в формулах, определяющих расстояния, требует наличия определенной априорной информации и не всегда может быть сделано оптимальных образом. Поэтому особый интерес представляют расстояния, в которых заложена идея выравнивания весов слагаемых от различных компонент, если они существенно отличаются по своим абсолютным значениям. Примером такого расстояния является расстояние по Камберру:

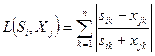(8)