Задание 1. 1. Выбираем из приложения к заданию 1 (стр
1. Выбираем из приложения к заданию 1 (стр. 4) массив финансовых показателей по которым будем оценивать финансовую устойчивость предприятия (Обязательно по одному показателю из каждой группы). Устанавливаем эталонные значения данных показателей в каждой группе риска в соответствие с предложенными диапазонами значений финансовых показателей (см. стр.4):
|
| x1
| x2
| x3
| x4
| | Показатели
| Эталоны
| | критическая зона
| зона опасности
| зона относительной стабильности
| зона благо-получия
| | Коэф. автономии
| 0.25
| 0.57
| 0.72
| 0.9
| | Коэф. абсолютной ликвидности
| 0.1
| 0.25
| 0.35
| 0.6
| | Общий коэф. оборачиваемости
| 0.2
| 0.5
| 0.7
|
| | Коэф. отношения чистых активов и уставного капитала
| 0.5
| 1.25
| 1.75
|
| | Рентабельность продаж
| 0.05
| 0.15
| 0.25
| 0.4
| 2. Задаем характеристики исследуемого предприятия. Веса показателям устанавливаются экспертами. Экспертом может выступать студент, выполняющий данную лабораторную работу:
|
| s
| n
| | Показатели
| Исследуемое предприятие
| Вектор весов показателей (выбирается экспертами)
| | Коэф. автономии
| 0.52
|
| | Коэф. абсолютной ликвидности
| 0.4
|
| | Общий коэф. оборачиваемости
| 0.49
|
| | Коэф. отношения чистых активов и уставного капитала
|
|
| | Рентабельность продаж
| 0.1
|
|
3. Рассчитываем разницу между составляющими векторов исследуемого предприятия и каждого эталонного образа:
| (s-xi)
| | 0.27
| -0.05
| -0.2
| -0.38
| | 0.3
| 0.15
| 0.05
| -0.2
| | 0.29
| -0.01
| -0.21
| -0.51
| | 1.5
| 0.75
| 0.25
| -1
| | 0.05
| -0.05
| -0.15
| -0.3
|
4. Рассчитываем квадрат разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа:
| (s-xi)^2
| | 0.0729
| 0.0025
| 0.04
| 0.1444
| | 0.09
| 0.0225
| 0.0025
| 0.04
| | 0.0841
| 0.0001
| 0.0441
| 0.2601
| | 2.25
| 0.5625
| 0.0625
|
| | 0.0025
| 0.0025
| 0.0225
| 0.09
|
5. Таким образом, расстояния по Эвклиду ( ) между исследуемым предприятием и эталонными образами будут равны: ) между исследуемым предприятием и эталонными образами будут равны:
|
| x1
| x2
| x3
| x4
| | Расстояние по Эвклиду
| 2.4995
| 0.5901
| 0.1716
| 1.5345
|
Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х3 (зона относительной стабильности).
6. Рассчитываем разницу между составляющими векторов исследуемого предприятия и каждого эталонного образа, возведенную в степень λ=4:
| (s-xi)^λ, λ=4
| | 0.00531441
| 6.25E-06
| 0.0016
| 0.02085136
| | 0.0081
| 0.000506
| 6.25E-06
| 0.0016
| | 0.00707281
| 1E-08
| 0.00194481
| 0.06765201
| | 5.0625
| 0.316406
| 0.00390625
|
| | 0.00000625
| 6.25E-06
| 0.00050625
| 0.0081
|
7. Таким образом, расстояния по Минковскому ( ) между исследуемым предприятием и эталонными образами будут равны: ) между исследуемым предприятием и эталонными образами будут равны:
|
| x1
| x2
| x3
| x4
| | Расстояние по Минковскому
| 5.08299347
| 0.316925
| 0.00796356
| 1.09820337
|
Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х3 (зона относительной стабильности).
8. Рассчитываем модуль разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа:
| |s-xi|
| | 0.27
| 0.05
| 0.2
| 0.38
| | 0.3
| 0.15
| 0.05
| 0.2
| | 0.29
| 0.01
| 0.21
| 0.51
| | 1.5
| 0.75
| 0.25
|
| | 0.05
| 0.05
| 0.15
| 0.3
|
9. Таким образом, расстояния по модулю разницы ( ) между исследуемым предприятием и эталонными образами будут равны: ) между исследуемым предприятием и эталонными образами будут равны:
|
| x1
| x2
| x3
| x4
| | Расстояние по модулю разности
| 2.41
| 1.01
| 0.86
| 2.39
|
Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х3 (зона относительной стабильности).
10. Рассчитываем произведение весов коэффициентов и квадрата разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа:
| nj*(s-xi)^2
| | 0.729
| 0.025
| 0.4
| 1.444
| | 0.63
| 0.1575
| 0.0175
| 0.28
| | 0.5046
| 0.0006
| 0.2646
| 1.5606
| |
| 2.25
| 0.25
|
| | 0.02
| 0.02
| 0.18
| 0.72
|
11. Таким образом, расстояния по Эвклиду с весами ( ) между исследуемым предприятием и эталонными образами будут равны: ) между исследуемым предприятием и эталонными образами будут равны:
|
| x1
| x2
| x3
| x4
| | Расстояние по Эвклиду (c весами)
| 10.8836
| 2.4531
| 1.1121
| 8.0046
|
Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х3 (зона относительной стабильности).
12. Рассчитываем произведение весов коэффициентов и разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа, возведенной в степень λ=4:
| nj*(s-xi)^λ, λ=4
| | 0.0531441
| 6.25E-05
| 0.016
| 0.2085136
| | 0.0567
| 0.003544
| 4.375E-05
| 0.0112
| | 0.04243686
| 6E-08
| 0.01166886
| 0.40591206
| | 20.25
| 1.265625
| 0.015625
|
| | 0.00005
| 5E-05
| 0.00405
| 0.0648
| 13. Таким образом, расстояния по Минковскому с весами ( ) между исследуемым предприятием и эталонными образами будут равны: ) между исследуемым предприятием и эталонными образами будут равны:
|
| x1
| x2
| x3
| x4
| | Расстояние по Минковскому (c весами)
| 20.402331
| 1.269281
| 0.04738761
| 4.69042566
|
Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х3 (зона относительной стабильности).
14. Рассчитываем произведение весов коэффициентов и модулей разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа:
| nj*|s-xi|
| | 2.7
| 0.5
|
| 3.8
| | 2.1
| 1.05
| 0.35
| 1.4
| | 1.74
| 0.06
| 1.26
| 3.06
| |
|
|
|
| | 0.4
| 0.4
| 1.2
| 2.4
| 15. Таким образом, расстояния по модулю разницы с весами ( ) между исследуемым предприятием и эталонными образами будут равны: ) между исследуемым предприятием и эталонными образами будут равны:
|
| x1
| x2
| x3
| x4
| | Расстояние по модулю разности (c весами)
| 12.94
| 5.01
| 5.81
| 14.66
|
Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х2 (зона опасности).
16. Рассчитываем сумму между составляющими векторов исследуемого предприятия и каждого эталонного образа:
| (s+xi)
| | 0.77
| 1.09
| 1.24
| 1.42
| | 0.5
| 0.65
| 0.75
|
| | 0.69
| 0.99
| 1.19
| 1.49
| | 2.5
| 3.25
| 3.75
|
| | 0.15
| 0.25
| 0.35
| 0.5
|
17. Рассчитываем модуль отношения (s-xi)/(s+xi) для каждой составляющей векторов исследуемого предприятия и каждого эталонного образа:
| |(s-xi)/(s+xi)|
| | 0.35064935
| 0.045872
| 0.161290323
| 0.267605634
| | 0.6
| 0.230769
| 0.066666667
| 0.2
| | 0.42028986
| 0.010101
| 0.176470588
| 0.342281879
| | 0.6
| 0.230769
| 0.066666667
| 0.2
| | 0.33333333
| 0.2
| 0.428571429
| 0.6
|
18. Таким образом, расстояния по Камберру (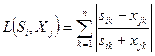 ) между исследуемым предприятием и эталонными образами будут равны: ) между исследуемым предприятием и эталонными образами будут равны:
|
| x1
| x2
| x3
| x4
| | Расстояние по Камберру
| 2.30427254
| 0.717511
| 0.899665673
| 1.609887513
|
Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х2 (зона опасности).
ВЫВОД: В результате проведенного анализа можно сделать вывод о том, что уровень финансовой устойчивости исследуемого предприятия характеризуется относительной стабильностью (согласно моделей 2-6 предприятие принадлежит к зоне х3 – относительная стабильность, модели 7-8 предприятие относят предприятия к зоне х2 – опасности).
|
| коэффициенты
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | вариант 1
| 0,19
| 0,76
| 0,05
| 0,44
| 0,41
| 0,51
| 0,9
| 1,74
| 0,4
| 0,64
| 0,14
| 0,64
| 0,05
| 2,48
| 0,3
| | вариант 2
| 0,47
| 0,92
| 0,2
| 0,34
| 0,19
| 0,54
| 0,69
| 4,94
| 0,28
| 1,3
| 0,15
| 2,18
| 0,05
| 0,07
| 0,08
| | вариант 3
| 0,91
| 0,64
| 0,03
| 0,25
| 0,26
| 0,92
| 0,22
| 1,69
| 0,79
| 0,36
| 0,01
| 1,55
| 0,19
| 2,82
| 0,27
| | вариант 4
| 0,09
| 0,63
| 0,09
| 0,27
| 0,08
| 0,98
| 0,58
| 3,89
| 0,83
| 1,81
| 0,01
| 0,17
| 0,14
| 0,92
| 0,26
| | вариант 5
| 0,45
| 0,36
| 0,09
| 0,33
| 0,92
| 0,56
| 0,81
|
| 0,36
| 1,46
| 0,1
| 0,18
| 0,19
| 1,63
| 0,47
| | вариант 6
| 0,57
| 0,34
| 0,06
| 0,05
| 0,65
| 0,65
| 0,51
| 3,87
| 0,83
| 0,09
| 0,06
| 0,23
| 0,11
| 0,41
| 0,27
| | вариант 7
| 0,26
| 0,3
| 0,16
| 0,35
| 0,03
| 0,73
| 0,2
| 3,19
| 0,57
| 1,55
| 0,09
| 1,37
| 0,1
| 2,55
| 0,21
| | вариант 8
| 0,14
| 0,16
| 0,16
| 0,35
| 0,27
| 0,7
| 0,09
| 4,36
| 0,45
| 1,45
| 0,06
| 2,47
| 0,08
| 2,88
| 0,13
| | вариант 9
| 0,22
| 0,15
| 0,15
| 0,36
| 0,53
| 0,24
| 0,4
| 0,51
| 0,62
| 1,42
| 0,09
| 0,94
| 0,2
| 1,55
|
| | вариант 10
| 0,03
| 0,34
| 0,17
| 0,18
| 0,04
| 0,45
| 0,2
| 3,91
| 0,6
| 1,93
|
| 0,53
| 0,01
| 0,21
| 0,11
| | вариант 11
| 0,37
| 0,02
| 0,19
| 0,46
| 0,13
| 0,21
| 0,03
| 3,31
| 0,21
| 1,44
| 0,09
| 0,54
| 0,13
| 2,77
| 0,21
| | вариант 12
| 0,03
| 0,49
| 0,19
| 0,2
| 0,55
| 0,78
| 0,03
| 1,22
| 0,64
| 0,64
| 0,17
| 1,21
|
| 1,82
| 0,12
| | вариант 13
| 0,12
| 0,69
| 0,04
| 0,47
| 0,7
| 0,58
| 0,45
| 1,32
| 0,81
| 1,71
| 0,19
| 2,96
| 0,14
| 0,31
| 0,27
| | вариант 14
| 0,11
| 0,26
| 0,14
| 0,46
| 0,73
| 0,66
| 0,67
| 2,92
| 0,25
| 0,95
| 0,11
| 1,09
| 0,01
| 1,75
| 0,26
| | вариант 15
| 0,97
| 0,07
| 0,11
| 0,42
| 0,58
| 0,86
| 0,83
| 0,7
| 0,5
| 1,45
| 0,1
|
| 0,07
| 1,28
| 0,15
| | вариант 16
| 0,63
| 0,78
| 0,05
| 0,04
| 0,15
| 0,14
| 0,98
| 0,35
| 0,67
| 0,85
| 0,15
| 0,95
| 0,18
| 2,01
| 0,34
| | вариант 17
| 0,36
| 0,31
| 0,14
| 0,47
| 0,92
| 0,59
| 0,5
| 1,18
| 0,82
| 0,16
| 0,16
| 1,92
| 0,06
| 0,39
| 0,49
| | вариант 18
| 0,6
| 0,94
| 0,18
| 0,01
| 0,58
| 0,31
| 0,34
| 1,64
| 0,37
| 0,6
| 0,14
| 1,81
| 0,17
| 2,68
| 0,23
| | вариант 19
| 0,9
| 0,09
|
| 0,43
| 0,9
| 0,06
| 0,85
| 4,6
| 0,53
| 1,78
| 0,06
| 1,8
| 0,06
| 1,94
| 0,01
| | вариант 20
| 0,06
| 0,47
| 0,08
| 0,47
| 0,31
| 0,36
| 0,63
| 2,39
| 0,84
| 1,7
| 0,16
| 1,47
| 0,12
| 0,42
| 0,16
| | вариант 21
| 0,27
| 0,78
| 0,09
| 0,16
| 0,96
| 0,65
| 0,89
| 2,33
| 0,28
|
| 0,02
| 0,73
| 0,05
| 2,05
| 0,28
| | вариант 22
| 0,21
| 0,58
| 0,02
| 0,23
| 0,51
| 0,69
| 0,78
| 3,25
| 0,93
| 1,3
| 0,12
| 2,24
| 0,19
| 1,11
| 0,25
| | вариант 23
| 0,15
| 0,97
| 0,06
| 0,16
| 0,58
| 0,67
| 0,62
| 1,17
| 0,21
| 1,12
| 0,12
| 0,33
| 0,12
| 1,77
| 0,23
| | вариант 24
| 0,03
| 0,47
| 0,08
| 0,28
| 0,33
| 0,39
| 0,02
| 2,58
| 0,46
| 1,46
| 0,2
| 2,37
| 0,08
| 2,36
| 0,16
| | вариант 25
| 0,73
| 0,48
| 0,19
| 0,31
| 0,4
| 0,42
| 0,56
| 0,25
| 0,94
| 1,22
| 0,03
| 1,85
| 0,08
| 0,02
| 0,18
| | вариант 26
| 0,47
| 0,63
| 0,09
| 0,24
| 0,54
| 0,51
| 0,4
| 2,15
| 0,33
| 1,61
| 0,17
| 0,03
| 0,1
| 2,01
| 0,15
| | вариант 27
| 0,69
| 0,76
| 0,13
| 0,2
| 0,92
| 0,92
| 0,91
| 1,87
| 0,85
| 1,68
| 0,18
| 1,56
| 0,18
| 0,18
| 0,32
| | вариант 28
| 0,47
| 0,73
| 0,11
| 0,13
| 0,21
| 0,5
| 0,24
| 1,91
| 0,22
| 0,86
| 0,07
| 0,41
| 0,1
| 0,59
| 0,21
| | вариант 29
| 0,13
| 0,8
| 0,13
| 0,39
| 0,74
| 0,27
| 0,53
| 1,83
| 0,06
| 1,21
| 0,13
| 2,01
| 0,15
| 2,55
| 0,07
| | вариант 30
| 0,77
| 0,18
| 0,09
| 0,2
| 0,42
| 0,58
| 0,67
| 3,99
| 0,71
| 0,09
| 0,02
| 1,36
|
| 1,43
| 0,17
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
Хронометражно-табличная методика определения суточного расхода энергии студента Цель: познакомиться с хронометражно-табличным методом определения суточного расхода энергии...
ОЧАГОВЫЕ ТЕНИ В ЛЕГКОМ Очаговыми легочными инфильтратами проявляют себя различные по этиологии заболевания, в основе которых лежит бронхо-нодулярный процесс, который при рентгенологическом исследовании дает очагового характера тень, размерами не более 1 см в диаметре...
Примеры решения типовых задач. Пример 1.Степень диссоциации уксусной кислоты в 0,1 М растворе равна 1,32∙10-2
Пример 1.Степень диссоциации уксусной кислоты в 0,1 М растворе равна 1,32∙10-2. Найдите константу диссоциации кислоты и значение рК.
Решение. Подставим данные задачи в уравнение закона разбавления
К = a2См/(1 –a) =...
|
РЕВМАТИЧЕСКИЕ БОЛЕЗНИ Ревматические болезни(или диффузные болезни соединительно ткани(ДБСТ))— это группа заболеваний, характеризующихся первичным системным поражением соединительной ткани в связи с нарушением иммунного гомеостаза...
Решение Постоянные издержки (FC) не зависят от изменения объёма производства, существуют постоянно...
ТРАНСПОРТНАЯ ИММОБИЛИЗАЦИЯ
Под транспортной иммобилизацией понимают мероприятия, направленные на обеспечение покоя в поврежденном участке тела и близлежащих к нему суставах на период перевозки пострадавшего в лечебное учреждение...
|
|

 ) между исследуемым предприятием и эталонными образами будут равны:
) между исследуемым предприятием и эталонными образами будут равны: ) между исследуемым предприятием и эталонными образами будут равны:
) между исследуемым предприятием и эталонными образами будут равны: ) между исследуемым предприятием и эталонными образами будут равны:
) между исследуемым предприятием и эталонными образами будут равны: ) между исследуемым предприятием и эталонными образами будут равны:
) между исследуемым предприятием и эталонными образами будут равны: ) между исследуемым предприятием и эталонными образами будут равны:
) между исследуемым предприятием и эталонными образами будут равны: ) между исследуемым предприятием и эталонными образами будут равны:
) между исследуемым предприятием и эталонными образами будут равны: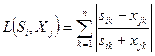 ) между исследуемым предприятием и эталонными образами будут равны:
) между исследуемым предприятием и эталонными образами будут равны:


