Решение. Пример 6. Найти частные производные второго порядка функции
Пример 6. Найти частные производные второго порядка функции Решение.
Таким образом:
Таким образом:
Заметим, что
Пример 7. Показать, что Решение. Сначала найдем первые частные производные
Теперь находим смешанные вторые частные производные и сравниваем их.
Экстремумы функции (максимум и минимум
а) Необходимые условия: если в точке
б) Достаточные условия: если
Пример 8. Найти минимум и максимум функции Решение. Найдем стационарные точки, в которых
Решим систему уравнений
+
Найдены три стационарные точки:
1) отсюда следует, что в точке
2) 3) отсюда следует, что в точке Ответ: Данная функция имеет минимум
Задача 5 Исследовать на экстремум функцию
|
Ответ: 
.
, 
,
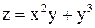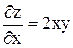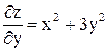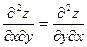при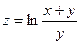 
.
Видим, что смешанные производные равны, что и требовалось показать.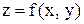
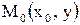функция имеет экстремум, то 
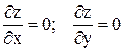в этой точке. 
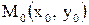– критическая (стационарная) точка.
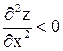в этой точке, то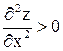 
, то 
, то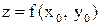 
.
.
(необходимые условия экстремума):
.
.
. Исследуем их на экстремум с помощью достаточных условий: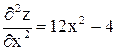
, 
, 
;
.
,
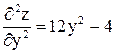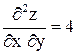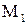функция z имеет минимум
.
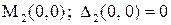– неизвестно, есть ли экстремум.
,
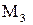функция z имеет минимум, 
.
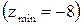в двух симметричных точках 
и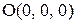 
у нее максимум 
.
.
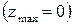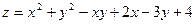