Решение. Найдем сначала стационарные точки, т.е
Найдем сначала стационарные точки, т.е. те точки, в которых частные производные одновременно равны нулю.
Изменим порядок во втором уравнении и приведем систему линейных уравнений к стандартному виду, чтобы ее можно было решить методом Крамера.
Нашли одну стационарную точку, в которой Выясним с помощью вторых производных, есть ли в
Составляем определитель Так как
Ответ:
Контрольные варианты к задаче 5. Исследовать на экстремум:
Элементы скалярного поля
Производная скалярного поля
 z
M β α
0 у
x Рис. 3
Пример 9. Найти скорость изменения скалярного поля Решение. Скорость изменения скалярного поля в направлении вектора
В задаче
Подставим все найденные величины в первую формулу:
Ответ: В заданном направлении данное скалярное поле убывает со скоростью
Градиент скалярного поля
Очевидно,
Рис. 7 Пример 10. Найти величину градиента скалярного поля
|
, это точка 
.
экстремум и, если есть, какой.
.
, то экстремум существует. Так как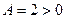 
, то в стационарной точке 
.
.
по направлению вектора
(рис.3).
определяется так: 
– это скорость изменения скалярного поля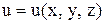 
в направлении вектора 
.
в точке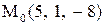 
в направлении от этой точки к точке 
.
определяют по формуле
.
, 
,
.
,
,
.
.
.
.
(рис. 7).
в точке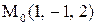 
.
