Решение.
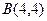Ответ: Задача 6. Найти производную функции Решение. Напишем формулу производной функции по направлению вектора
Сначала найдем вектор Теперь найдем частные производные функции
Все найденные значения подставляем в формулу производной по направлению.
Вывод. Функция Ответ: Контрольные варианты к задаче 6. Найти производную функции:
Задача 7 Найти формулу вида
Решение. Нужно провести прямую
Перепишем эти уравнения так, чтобы потом можно было решить полученную систему линейных уравнений относительно
Внизу получились в результате суммирования нужные коэффициенты. Подставляем их в систему:
Контрольные варианты к задаче 7.
|
.
.
.
в точке 
в направлении от этой точки к точке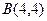 
.
.
, где 
- орт направления вектора 
= 
. Найдем длину 
. Направляющие косинусы вектора 
.
.
, так как полученная производная меньше нуля.
в точке (3; 1) в направлении от этой точки к точке (6; 5).
в точке (4; 1) в направлении от этой точки к точке (5; 1).
в точке (2; 1) в направлении от этой точки к началу координат.
в точке (1; 1) в направлении от этой точки к точке (2; 2).
в точке (1; 2) в направлении от этой точки к точке (1; 1).
в точке (5; 1) в направлении от этой точки к точке (9; 4).
в точке (1; 2) в направлении вектора, образующего с осью OX угол в 45о.
в точке (1; 1) в направлении, образующем углы α = 30о, β = 60о.
в точке (1; 1) в направлении биссектрисы 1-го координатного угла.
в точке (1; 2) в направлении, составляющем с осью OX угол в 60о.
в точке (1; 1) по направлению вектора 
.
в точке (1; 1) в направлении луча, образующего угол в 60о с осью ОХ.
в точке (1; 1) в направлении биссектрисы 1-го координатного угла.
в точке (3; 1) по направлению вектора 
.
методом наименьших квадратов по данным опыта.
, которая зависит от двух переменных 
и 
и находится точка ее минимума.
. Это можно записать короче: 
. Находим стационарную точку.
. Ответ: 
