Дифференцирование функций нескольких переменных
Частные производные функции а) первого порядка: где
где б) второго порядка:
Можно показать, что порядок дифференцирования безразличен, т. е.
Правило. Отыскивая частные производные функции нескольких переменных по одной из переменных, пользуемся правилами и формулами дифференцирования, считая в этот момент все остальные переменные постоянными. Пример 3. Найти частные производные первого порядка следующих функций: а)
отыскивая
отыскивая
б)
отыскивая
отыскивая Пример 4. Доказать следующие тождества: а) Решение. Найдем
отыскивая
отыскивая Следовательно
что и требовалось доказать. Пример 5. Найти
|
,
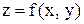
- частное приращение z по х.
,
- частное приращение z по y.
- вторая производная функции z по переменной x, т. е. частная производная по переменной х, взятая от частной производной первого порядка по переменной х.
- смешанная производная z по х и по у;
;
- вторая производная функции z по переменной y.
.
,
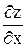, переменную у считаем постоянной.
,
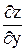, переменную х считаем постоянной.
.
, если 
.
данной функции и подставим их в равенство, которое надо доказать:
,
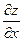и 
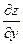функции 
.
