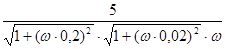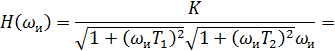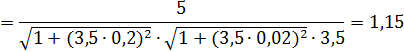Задача 2. Расчет частотных характеристик линейных САУ.
Определить круговую частоту ω, с которой устройство САУ, состоящее из последовательно включенных двух апериодических и одного идеального интегрирующего звеньев, дает заданный сдвиг по фазе между выходным и входным сигналами. При этом следует определить амплитуду выходного сигнала Y mна данной частоте, если известна амплитуда входного сигнала X m. Передаточная функция заданной САУ имеет следующий вид:
Решение. По передаточной функции W (p), представленной в операторной форме, найдем выражение для частотной передаточной функции W (j ω) путем замены в выражении (10) оператора Лапласа р на комплексную переменную j ω.
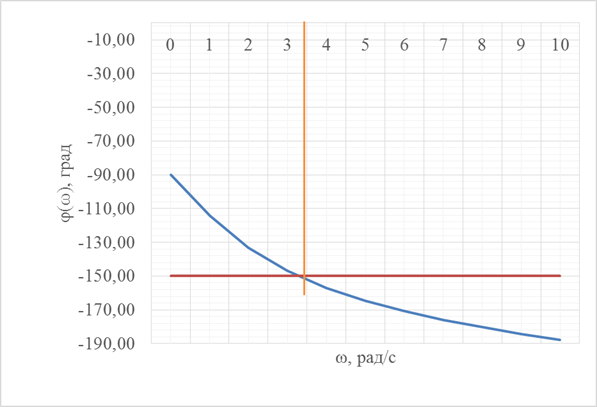
W (j ω) = где: Н (ω) = Н (ω) = φ(ω) = - 90о – arctg(ω∙ T 1) - arctg(ω∙ T 2) – аргумент частотной передаточной функции, представляющий собой фазочастотную характеристику (ФЧХ) системы САУ. Задаваясь значениями круговой частоты ω с шагом 1-2 рад/с определим значения функции φ(ω), занесем их в таблицу расчетных значений и построим график ФЧХ, на котором проведем горизонтальную прямую через точку, соответствующую заданному углу сдвига фаз φ = -150о, до пересечения с кривой ФЧХ. Через найденную точку пересечения проведем горизонтальную прямую до пересечения с осью частот, на которой отметим искомую круговую частоту ωи, которая дает заданный табл. 2 сдвиг фазы φ(ωи) = - 1500. ωи = 3,5 рад/с. Таблица 2.1
Рис. 2.1. График ФЧХ.
Подставляя найденное значение круговой частоты ωи в выражение для модуля Н (ω) частотной передаточной функции, вычислим его значение Н (ωи).
Затем определяем искомую амплитуду выходного сигнала: Ym = H (ωи) Хт = 1,15 ∙ 2 = 2,3
|

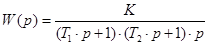 . (10)
. (10)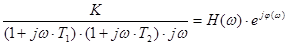 , (11)
, (11)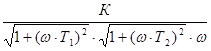 - модуль частотной передаточной функции, представляющий собой амплитудно-частотную характеристику (АЧХ) системы САУ;
- модуль частотной передаточной функции, представляющий собой амплитудно-частотную характеристику (АЧХ) системы САУ;