Задача 3. Построение логарифмических частотных характеристик и годографа АФЧХ.
1. Построить асимптотическую логарифмическую амплитудно-частотную характеристику (ЛАЧХ) и логарифмическую фазочастотную характеристику ЛФЧХ для линейной системы САУ, состоящей из четырех последовательно включенных звеньев: одного реального дифференцирующего звена с передаточной функцией W 1(р) = К 1∙(Т 1∙ р + 1);
двух апериодических звеньев первого порядка с передаточными функциями W 2(р) = К 2/(Т 2∙ р + 1) и W 3(р) = К 3/(Т 3∙ р + 1);
одного идеального интегрирующего звена с передаточной функцией К 4/ р. По условиям задачи передаточная функция заданной линейной САУ имеет следующий вид:
где К = К 1∙ К 2∙ К 3∙ К 4.
2. Построить годограф АФЧХ W (j ω) заданной САУ.
Решение. Найдем выражение для логарифмической АЧХ и ФЧХ, для чего сначала определим АФЧХ системы по ее передаточной функции W (р), заменяя в ней оператор Лапласа р на комплексную переменную j ω. W (j ω) =
где: Н (ω) = φ(ω) = [- 90о + arctg(ω∙ T 1) - arctg(ω∙ T 2) - arctg(ω∙ T 3)] – аргумент частотной передаточной функции, представляющий собой фазочастотную характеристику (ФЧХ) системы САУ. По известной АЧХ определим выражение для ЛАЧХ L (ω): L (ω) = 20∙lg H (ω) = = Асимптотическую ЛАЧХ строим путем замены непрерывной кривой ЛАЧХ несколькими прямыми отрезками, которые сопрягаются между собой в точках, соответствующих круговым частотам ωс (сопрягающим частотам), численно равным обратной величине от постоянных времени, входящих в выражение (14). Мы имеем три сопрягающие частоты: ωс1 = 1/ Т 1, рад/с; ωс2 = 1/ Т 2, рад/с; ωс3 = 1/ Т 3, рад/с.
Расположим сопрягающие частоты в порядке возрастания при следующих исходных данных нашего примера: К = 4; Т 1 = 0,5 с; Т 2 = 0,2 с; Т 3 = 0,02 с. Учитывая, что чем больше значение постоянной времени, тем меньше значение сопрягающей частоты, можем написать следующее неравенство: ωс1 = 2< ωс2 = 5 < ωс3 = 50 рад/с. Выбираем масштаб для одной декады частот так, чтобы в этом масштабе на оси абсцисс (частот) разместить три декады логарифмической шкалы. Так, как значения всех сопрягающих частот больше 1 (ωс ≥ 1рад/с), то в качестве границ декад выбираем круговые частоты 1, 10, 100 и 1000 рад/с. В пределах каждой декады можно выделить промежуточные значения частот, используя для этих целей логарифмическую шкалу. Затем на логарифмической оси частот отмечаем точки, соответствующие сопрягающим частотам ωс1,ωс2, ωс3,и проводим через них вертикальные пунктирные линии. Ось ординат проводим через частотную отметку 1 рад/с и выбираем соответствующий масштаб, исходя из значения величины 20∙lg K, так, чтобы можно было отложить значения (20∙lg K + 20) и (20∙lg K - 40), дБ. На оси ординат следующие точки:
20∙lg4 = 12; 20∙lg4 + 20 = 32; 20∙lg4 – 40 = -27,9 дБ. С целью удобства построения асимптотической JIA4X выбираем масштаб 1 см на 10 дБ. Проводим через точку 20lg K вправо от оси ординат прямую линию с наклоном -20 дБ на декаду, для чего соединяем эту точку с точкой (20lg К - 20), расположенной на частотной отметке 10 рад/с. На отрезке логарифмической оси частот 1 < ω <
Первая сопрягающая частота
Вторая сопрягающая частота
и, следовательно, ее наклон увеличивается на -20 дБ/дек и становится вновь равным -20 дБ/дек. Соединяя ординату
Третья сопрягающая частота
и, следовательно, ее наклон вновь увеличивается на -20 дБ/дек и становится равным -40 дБ/дек. Соединяя ординаты На рисунке 1 показан график асимптотической ЛАЧХ, построенный в соответствии с вышеприведенным алгоритмом.
Рис. 2. График логарифмической ФЧХ.
Для построения логарифмической ФЧХ воспользуемся выражением: φ(ω) = - 90° + arctg( Задаваясь численными значениями круговой частоты от 1 до 1000 рад/с, заполним соответствующий столбец табл. 4 значениями частотной функции φ(ω) и выполним ее построение на рисунке 2.
Для построения годографа АФЧХ необходимо также заполнить соответствующие столбцы табл. 4, для чего необходимо произвести расчет модуля Н (ω) частотной передаточной функции W (j ω) и его проекций на мнимую (М (ω) = Н (ω)∙sin[φ(ω)]) и действительную (N (ω) = Н (ω)∙cos[φ(ω)]), Н (ω) = а также использовать данные выполненного ранее расчета фазочастотной характеристики. Таблица 1.2
Рис. 3. Годограф АФЧХ. Способ построения годографа АФЧХ основан на использовании полярных координат, для чего на комплексной плоскости через начало ее координат проводят ряд линий под углами, взятыми из табл 1.4. для соответствующих частот, и на этих линиях откладывают в произвольно выбранном масштабе значения модуля Н(ω) АФЧХ. Соединяя затем концы векторов между собой и с началом координат, получим искомый фрагмент годографа АФЧХ. Рекомендуемая литература. 1. Ротач В.Я. Теория автоматического управления: Учеб. для вузов. — М.: МЭИ, 2006. 2. Теория автоматического управления/ Под ред. А.А. Воронова. Ч. 1 и 2. — М.: Высшая школа, 1986. 3. Ерофеев А.А. Теория автоматического управления: Учеб. для вузов. - 2005. 4. Юревич Е.И. Теория автоматического управления. — СПб.: ВЕГУ -Санкт- Петербург, 2007.
|
, (12)
, (13)
- амплитудно-частотная характеристика (АЧХ) системы САУ;
, дБ (14)
асимптотическая ЛАЧХ описывается выражением: 
20lg К - 20lgω и представляет собой отрезок проведенной ранее прямой с наклоном -20 дБ/дек, соединяющий точки ее пересечения с вертикальными пунктирными линиями, проведенными из точек 1 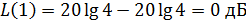и 
и
≤ 
описывается выражением 
и, следовательно, ее наклон уменьшается на 20 дБ/дек и становится равным 0 дБ/дек. Соединяя ординаты 
в точке 
) = 
описывается выражением: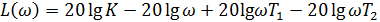
= 
дБ, получив на отрезке логарифмической оси частот 
> 
в точке 
Рис. 1. График асимптотической ЛАЧХ.
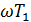) - arctg(
) - arctg(
).
