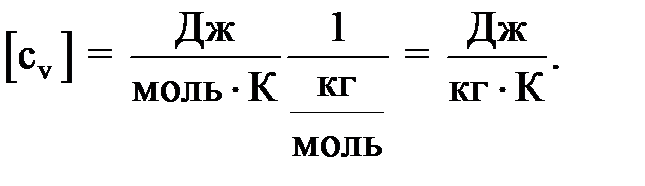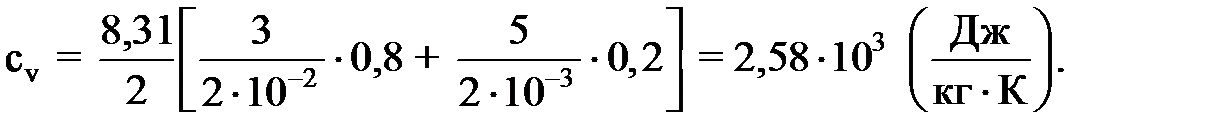ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. З а д а ч а 1. Небольшие санки массой 3 кг при помощи веревки длиной 1,5 м тянут с постоянной скоростью вверх по наклонной плоскости
З а д а ч а 1. Небольшие санки массой 3 кг при помощи веревки длиной 1,5 м тянут с постоянной скоростью вверх по наклонной плоскости, составляющей с горизонтом угол 30° (рис. 1). К веревке (вдоль нее) прикладывают силу в 21 Н. Расстояние от свободного конца веревки до наклонной плоскости равно 1 м (веревка прикреплена к центру масс санок). Найти коэффициент трения скольжения санок о поверхность плоскости.
   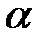 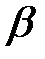
Санки, участвующие в поступательном движении, примем за материальную точку. Согласно основному уравнению динамики частицы (второму закону Ньютона) имеем:
(в инерциальной системе отсчета произведение массы частицы на ее ускорение равно векторной сумме всех сил, действующих на эту частицу). На санки действуют (см. рис. 1) силы: Выбираем инерциальную систему отсчета, связывая ее с неподвижной наклонной плоскостью так, чтобы ось ОХ была направлена в сторону движения тела. Находим проекции всех векторов уравнения движения на координатные оси:
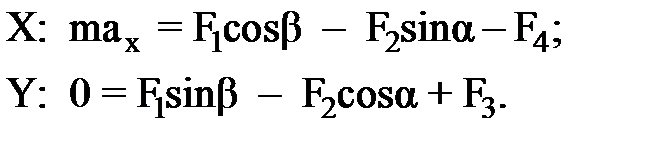
Учитывая, что ускорение равно нулю (санки движутся с постоянной скоростью),

получаем:
Проверяем единицу измерения:
Производим вычисления:
Ответ: З а д а ч а 2. С какой силой следует прижимать тормозную колодку к колесу, вращающемуся с частотой 30 об/с, для его остановки в течение 20 с, если коэффициент трения между колодкой и ободом колеса равен 0,5? Колесо (рис. 2) имеет форму сплошного диска массой 10 кг и диаметром 0,2 м. Сколько оборотов сделает колесо до остановки?
Колесо участвует во вращательном движении относительно неподвижной оси, проходящей через центр масс (центр инерции) тела. Согласно основному уравнению динамики вращательного движения имеем:
(в инерциальной системе отсчета произведение момента инерции твердого тела относительно центра масс на его угловое ускорение равно векторной сумме моментов всех внешних сил, действующих на это тело относительно центра масс).На колесо действуют (см. рис. 2) силы: тяжести Выбираем инерциальную систему отсчета, связывая ее с неподвижной осью вращения так, чтобы ось OZ была направлена вдоль оси вращения (при этом используем «правило буравчика»). Находим проекцию всех векторов уравнения движения на координатную ось OZ:
(проекции моментов сил Колесо имеет форму сплошного диска, тогда момент инерции
Движение колеса вращательное равнопеременное, поэтому для решения задачи воспользуемся формулами:
Учитывая, что колесо остановится
И, наконец, Тогда окончательно имеем:
отсюда Проверяем единицу измерения:
Производим вычисления:
Количество оборотов N, которое сделает колесо до остановки за 20 с, вычисляем через полный угол поворота колеса:
отсюда
Проверяем единицу измерения:
Производим вычисления:
Ответ: F3 = 9,4 Н; N = 300 об. З а д а ч а 3. Налетев на пружинный буфер, вагон массой 16 т, двигавшийся со скоростью 0,6 м/с, остановился, сжав пружину на 8 см. Найти общую жесткость пружин буфера. Насколько бы деформировались пружины при уменьшении скорости вагона в два раза?
Отсюда:
Проверяем единицу измерения:
Производим вычисления:
Во втором случае вагон остановился не полностью, поэтому в потенциальную энергию буферных пружин перешла только часть кинетической энергии. С учетом этого запишем:
Отсюда
Проверяем единицу измерения:
Производим вычисления:
Ответ: З а д а ч а 4. Небольшой ящик массой 20 кг соскальзывает по идеально гладкому лотку длиной 2 м на неподвижную тележку с песком (рис. 3) и застревает в нем. Тележка с песком массой 80 кг может свободно (без трения) перемещаться по рельсам в горизонтальном направлении. Определить скорость тележки с ящиком, если лоток наклонен под углом 30° к рельсам.
Тележку и ящик можно рассматривать как систему двух неупруго взаимодействующих тел. Эта система не замкнута, так как сумма внешних сил (см. рис. 3), действующих на систему (сил тяжести
где Учитывая, что тележка до взаимодействия с ящиком покоилась (р2x = 0), а после взаимодействия оба тела системы движутся с одной скоростью
Скорость ящика перед падением на тележку v1 определяем из закона сохранения механической энергии:
где Решая уравнения (2) и (3) совместно относительно
Проверяем единицу измерения:
Производим вычисления:
Ответ:
З а д а ч а 5. Платформа в виде сплошного диска радиусом 1,5 и массой 180 кг вращается по инерции вокруг вертикальной оси, делая 12 об/мин. В центре платформы стоит человек массой 60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
где I1 и I2 – моменты инерции платформы и человека в начальном состоянии системы; Найдя проекции всех величин, входящих в векторное уравнение (1), относительно инерциальной системы отсчета (ось OZ совпадает с геометрической осью вращения платформы), запишем закон сохранения момента импульса в скалярной форме:
Момент инерции платформы относительно оси OZ при переходе человека не изменяется:
Момент инерции человека относительно той же оси будет изменяться. Если рассматривать человека как материальную точку, то его момент инерции в начальном положении (в центре платформы) I2z можно считать равным нулю. В конечном положении (на краю платформы) момент инерции человека
Учитывая сказанное выше и то, что
После сокращения на R2 и простых преобразований находим:
Проверяем единицу измерения:
Производим вычисления:
Ответ: v = 1,13 м/с.
З а д а ч а 6. В цилиндре под поршнем находится водород массой 20 г при температуре 27°С. Водород сначала расширился адиабатно, увеличив свой объем в пять раз, а затем был сжат изотермически до первоначального объема. Найти изменение внутренней энергии газа, работу, совершенную газом в этих процессах, и количество теплоты, подведенной к газу в этих процессах. Изобразить процессы в диаграмме «давление – объем».
Изменение внутренней энергии идеального газа в процессе 1 – 3 вычисляется по формуле:
где i – число степеней свободы молекул двухатомного газа водорода Н2; Т3 = Т2, так как процесс 2 – 3 изотермический. При адиабатном процессе 1 – 2 температура и объемы газа связаны между собой уравнением: T1V1γ - 1 = T2V2γ - 1, (2) где отсюда Т3 = Т2 = Т1 (V1/V2)γ - 1. (3) Тогда общее изменение внутренней энергии газа
Проверяем единицу измерения:
Производим вычисления:
Так как в изотермическом процессе 2 – 3 ΔWвн равна нулю, работу А1-2 газа при адиабатном расширении 1 – 2 вычисляем по формуле: А1-2 = −ΔWвн1-2 = − ΔWвн1-3; (5) А1-2 = 29,6 кДж. Работу А2-3 при изотермическом сжатии 2 – 3 рассчитываем по урав-нению:
Проверяем единицу измерения:
Производим вычисления:
Следовательно, полная работа, совершаемая газом, А1-3 = А1-2 + А2-3; (7) А1-3 = 29,6 − 21,1 = 8,5 (кДж). Согласно первому закону термодинамики теплота Q, переданная газу, равна сумме изменения внутренней энергии ΔWвн и работы А: Q = ΔWвн + A1-3; (8) Q = -29,6 + 8,5 = −21,1 кДж. Ответ: ΔWвн = −29,6 кДж; A1-3 = 8,5 кДж; Q = −21,1 кДж (тепло отводится). З а д а ч а 7. Два килограмма льда, находящегося при температуре -13оС, нагрели и превратили в пар. Определить изменение энтропии в этом процессе.
Общее изменение энтропии ΔS равно сумме изменений энтропии, происходящих на отдельных стадиях процесса: ΔS = ΔS1 + ΔS2 + ΔS3 + ΔS4. (1) Процесс нагревания твердого вещества (льда) происходит при неизменном объеме (δA = 0), следовательно, изменение энтропии в этом процессе
где с1 – удельная теплоемкость льда (в этой области температуры с1 = const = = 2100 Дж/(кг·К)). Изменение энтропии ΔS2 при плавлении льда (Т2 = const)
где λ - удельная теплота плавления льда, λ = 330 кДж/кг. Изменение энтропии ΔS3 при нагревании воды от Т1 до температуры кипения Т3 (процесс происходит без изменения объема) рассчитываем по формуле:
где с2 – удельная теплоемкость воды (в этой области температуры с2 = const = = 4190 Дж/(кг·К)). И, наконец, изменение энтропии ΔS4 при превращении воды в пар
где r – удельная теплота парообразования воды, r = 2,25 МДж/кг. Таким образом, общее изменение энтропии в данном процессе
Проверяем единицу измерения:
Производим вычисления:
Ответ: ΔS = 17,3 кДж/К. З а д а ч а 8. Вычислить удельную теплоемкость смеси неона и водорода при постоянном объеме с ν v, если массовые доли неона и водорода составляют соответственно 80 и 20 %.
Q = (m1с ν v1 + m2с ν v2)ΔT, (2) где с ν v1, с ν v2 - удельная теплоемкость неона и водорода соответственно,
Приравнивая правые части уравнений (1), (2) друг к другу и разделив обе части полученного равенства на ΔТ, получаем:
отсюда
Проверяем единицу измерения:
Производим вычисления:
Ответ: сv = 2,58 кДж/(кг·К).
ТАБЛИЦА ВАРИАНТОВ И НОМЕРА ЗАДАЧ К КОНТРОЛЬНОЙ РАБОТЕ № 1
ЗАДАЧИ
|

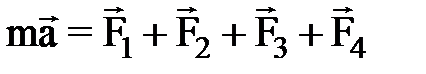 (1)
(1)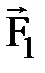 , направленная под углом β; к перемещению, тяжести
, направленная под углом β; к перемещению, тяжести  , реакции опоры
, реакции опоры 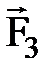 и трения
и трения 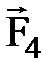 .
.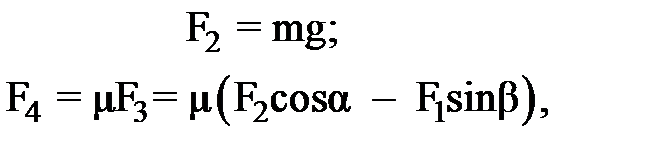
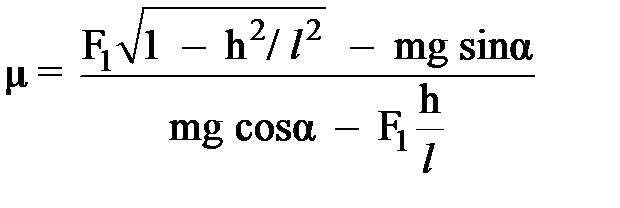 . (8)
. (8)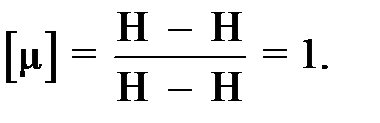
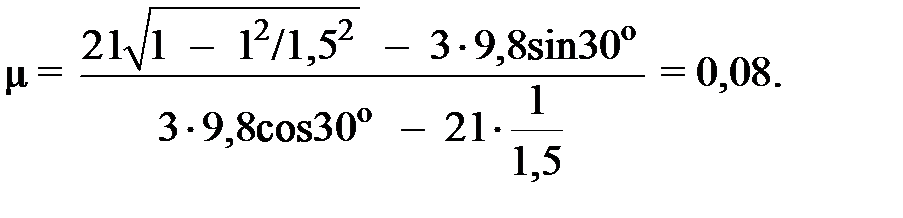
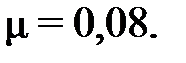
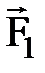

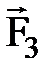

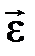
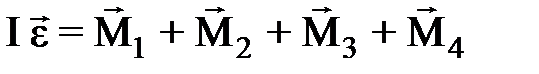 (1)
(1) , реакции опоры
, реакции опоры 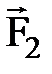 ,
, 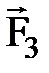 , с которой прижимают к колесу тормозную колодку, и трения
, с которой прижимают к колесу тормозную колодку, и трения 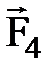 между колодкой и ободом колеса (трением на оси колеса можно пренебречь).
между колодкой и ободом колеса (трением на оси колеса можно пренебречь). (2)
(2)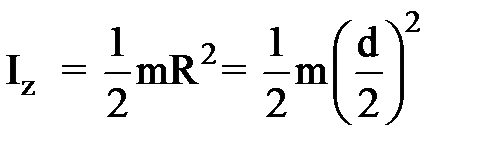 . (3)
. (3)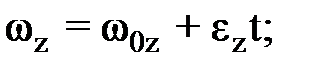 (4)
(4)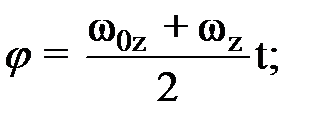 (5)
(5)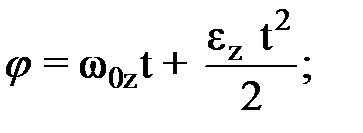 (6)
(6)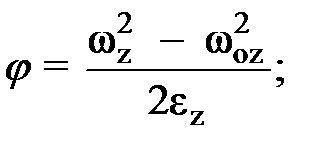 (7)
(7)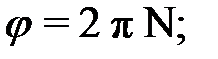 (8)
(8)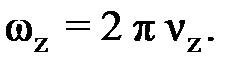 (9)
(9) , получаем:
, получаем: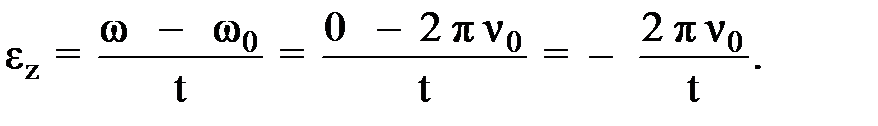 (10)
(10)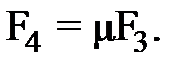
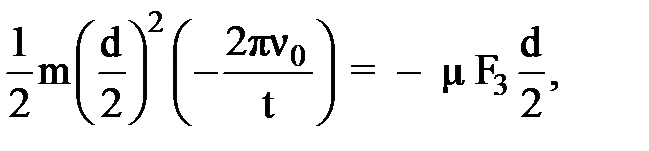 (11)
(11)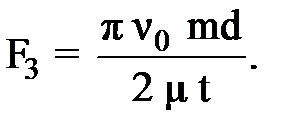
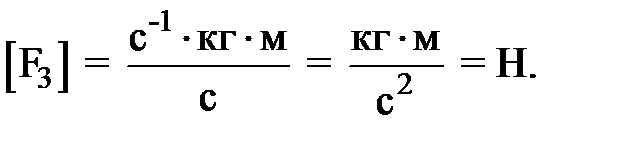

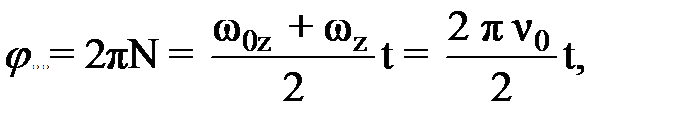 (12)
(12)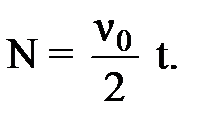 (13)
(13)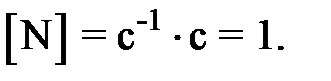

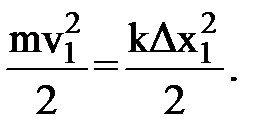 (1)
(1)
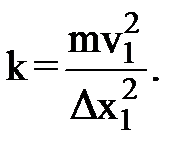 (2)
(2)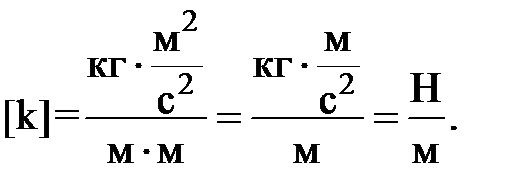

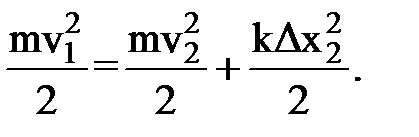 (3)
(3)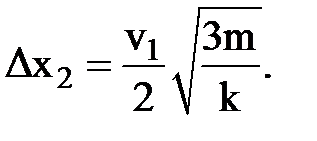 (4)
(4)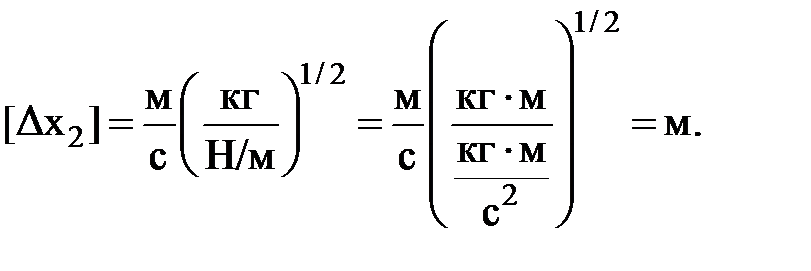
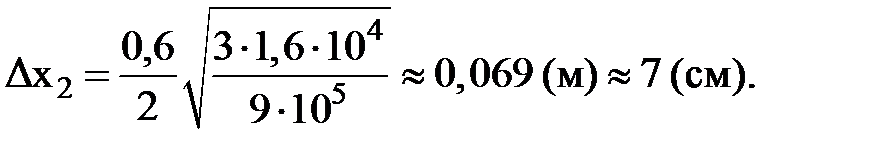
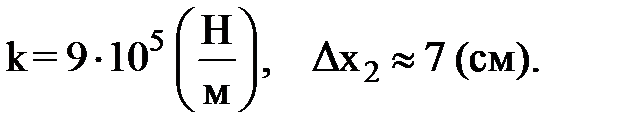
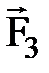
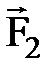
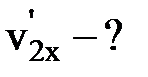
 и
и 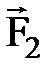 и силы реакции опоры
и силы реакции опоры  ), не равна нулю, поэтому применить закон сохранения импульса к системе «ящик – тележка» нельзя, но так как проекция суммы указанных сил на ось ОХ инерциальной системы, совпадающей с направлением рельсов, равна нулю, то проекцию импульса системы на это направление можно считать постоянной, т. е.
), не равна нулю, поэтому применить закон сохранения импульса к системе «ящик – тележка» нельзя, но так как проекция суммы указанных сил на ось ОХ инерциальной системы, совпадающей с направлением рельсов, равна нулю, то проекцию импульса системы на это направление можно считать постоянной, т. е.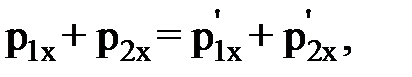 (1)
(1)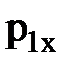 и
и 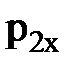 – проекции импульса ящика и тележки с песком в момент падения ящика на тележку;
– проекции импульса ящика и тележки с песком в момент падения ящика на тележку; 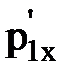 и
и 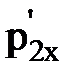 – то же после падения ящика.
– то же после падения ящика.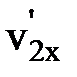 , получаем:
, получаем: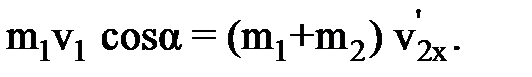 (2)
(2)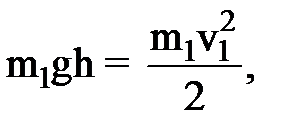 (3)
(3)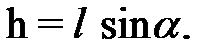
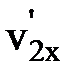 , получаем:
, получаем: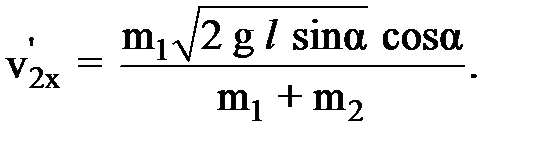 (4)
(4)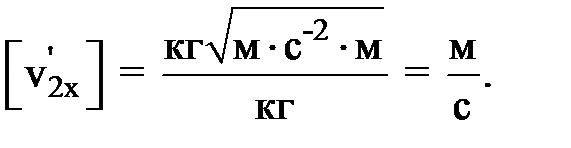
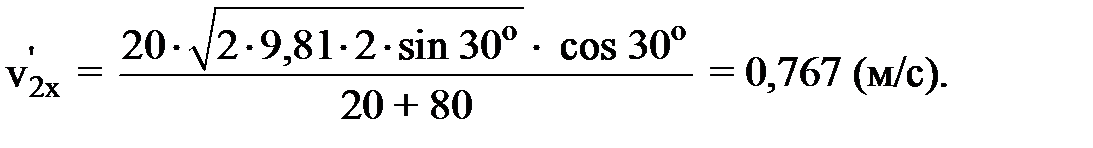
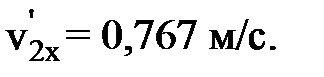
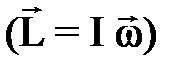 системы «платформа – человек» относительно оси OZ остается постоянным:
системы «платформа – человек» относительно оси OZ остается постоянным:
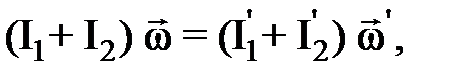 (1)
(1)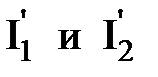 – моменты инерции платформы и человека в конечном сос-тоянии системы (после перехода на край платформы);
– моменты инерции платформы и человека в конечном сос-тоянии системы (после перехода на край платформы);  – угловая скорость вращения системы в начальном и конечном состоянии.
– угловая скорость вращения системы в начальном и конечном состоянии.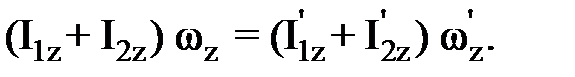 (2)
(2)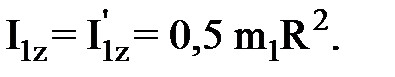 (3)
(3)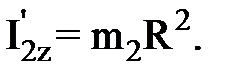 (4)
(4)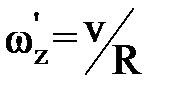 (v – линейная скорость человека относительно пола), получаем:
(v – линейная скорость человека относительно пола), получаем: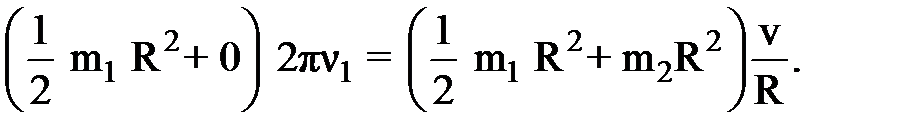 (5)
(5)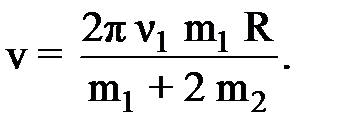 (6)
(6)

 (1)
(1)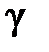 - адиабатная постоянная для двухатомного газа водорода,
- адиабатная постоянная для двухатомного газа водорода, 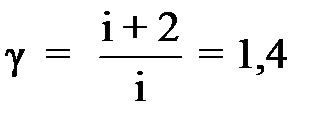 ,
,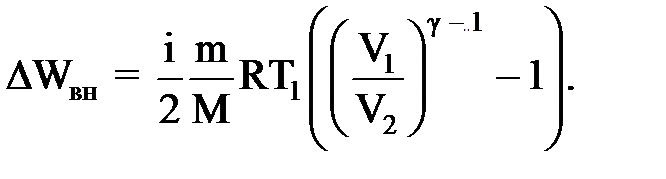 (4)
(4)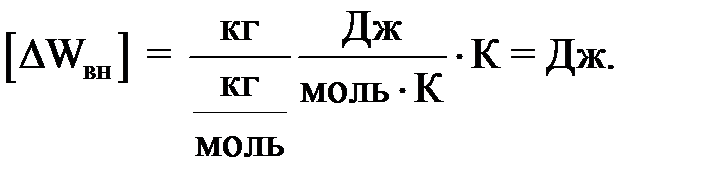
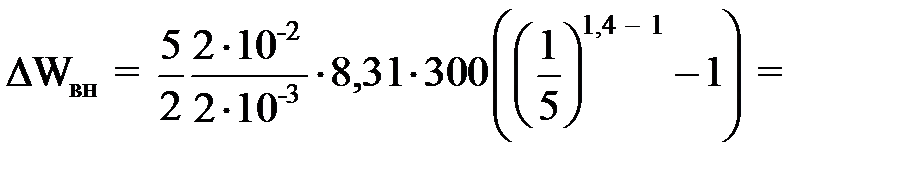 -29,6 (кДж).
-29,6 (кДж).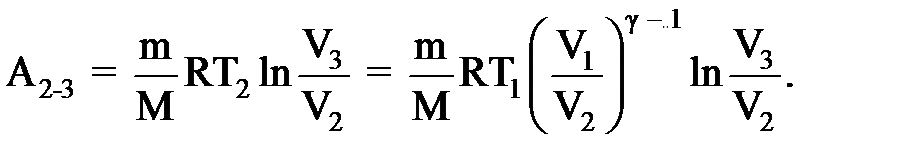 (6)
(6)
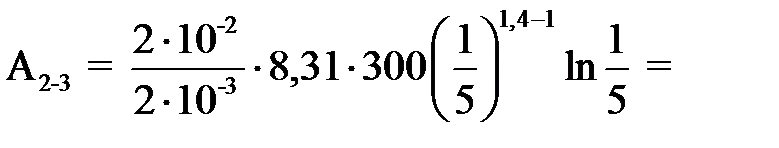 -21,1 (кДж).
-21,1 (кДж).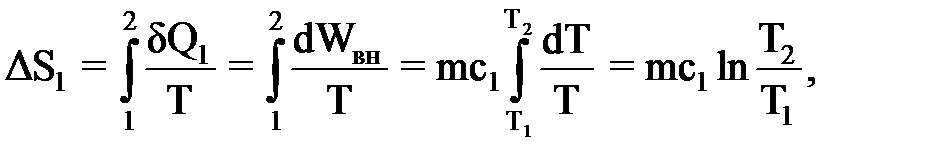 (2)
(2)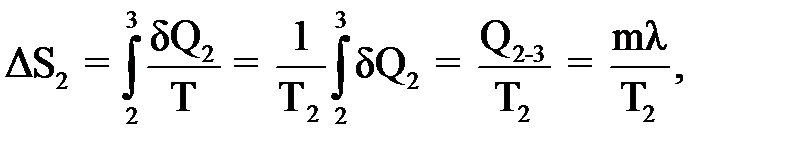 (3)
(3)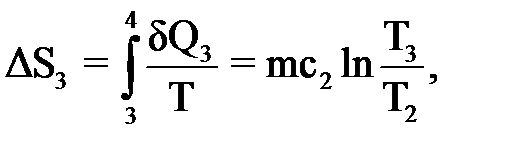 (4)
(4)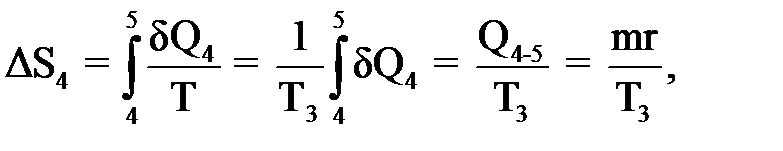 (5)
(5)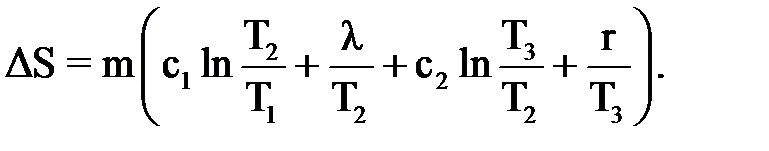 (6)
(6)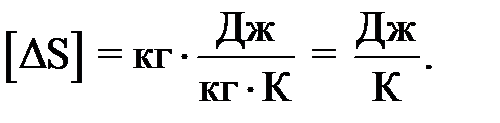
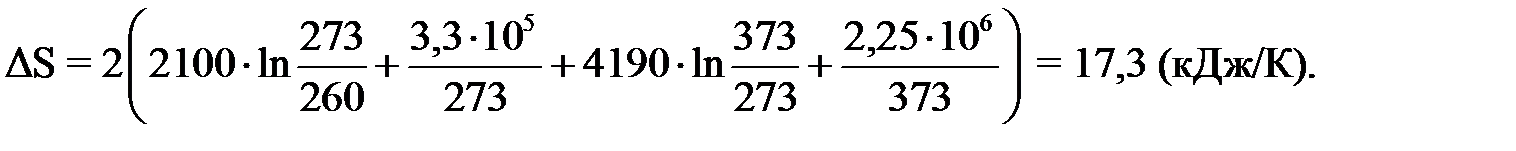
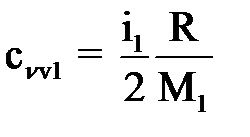 ; (3)
; (3) . (4)
. (4) , (5)
, (5)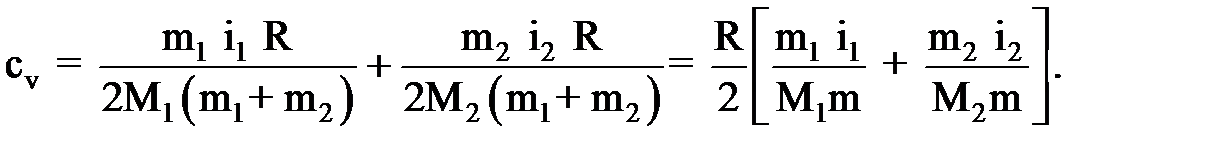 (6)
(6)