Задано эмпирическое распределение непрерывной случайной величины в виде последовательности интервалов и соответствующих им частот , причем (объем выборки). Требуется, используя критерий Пирсона, проверить гипотезу о том, что случайная величина X распределена равномерно.
Правило. Для того чтобы проверить гипотезу о равномерном распределении , т.е. по закону
надо:
1. Оценить параметры и - концы интервала, в котором наблюдались возможные значения , по формулам (через и обозначены оценки параметров)
.
2. Найти плотность вероятности предполагаемого распределения
.
3. Найти теоретические частоты:
.
4. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы , где - число интервалов, на которые разбита выборка.
Задача №658. Произведено n=200 испытаний, в результате каждого из которых событие А появлялось в различные моменты времени. В итого было получено эмпирическое распределение, приведенное в табл.1(в первой строке указаны интервалы времени в минутах, во второй – соответствующие частоты, т.е. число появления А в интервале). Требуется при уровне значимости 0,05 проверить гипотезу о том, что время появления событий распределено равномерно.
Таблица 13
интервал
2-4
4-6
6-8
8-10
10-12
12-14
14-16
16-18
18-20
20-22
частота
Составим гистограмму
Рис. 1
По виду гистограммы частоты отклоняются от некоторой прямой. Предположим, что имеем равномерное распределение.
Решение 1. Найдем оценки параметров и равномерного распределения по формулам: ,
Для вычисления выборочной средней и выборочного среднего квадратического отклонения примем середины интервалов в качестве вариант (наблюдаемых значений X). В итоге получим эмпирическое распределение равноотстоящих вариант:
Таблица 14
№ п/п
2-4
4-6
6-8
8-10
10-12
12-14
14-16
16-18
18-20
20-22
Таблица 15
№ п/п
∑
Пользуясь, например, методом произведений, найдем:
Следовательно:
2. Найдем плотность предполагаемого равномерного распределения:
3. Найти теоретические частоты:
Длины третьего-девятого интервалов равны длине второго интервала, поэтому теоретические частоты, соответствующие этим интервалам и теоретическая частота второго интервала одинаковы, т.е.
.
4. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы . Для этого составим таблицу.
Таблица 16
i
17,4
3,7
13,69
0,79
-4
0,80
-5
1,25
1,80
0,20
-6
1,80
0,05
0,20
-2
0,20
23,6
1,4
1,96
0,08
∑
Из расчетной таблицы получаем . По таблице находим . Так как < нет оснований отвергать гипотезу о равномерном распределении. Данные наблюдений согласуются с этой гипотезой.
Контрольные вопросы.
1. Что называется статистической гипотезой?
2. Какие критерии согласия вы знаете?
3. Как определяется число степеней свободы? В каком критерии оно используется?
4. Когда необходимо объединять интервалы?
5. Можно ли использовать критерий , если имеется 20 опытных данных?
6. Может ли критерий согласия давать согласие с несколькими законами распределения?
Библиографический список.
1. Гмурман В.Е. Теория вероятности и математическая статистика. М.: Высшая школа, 2002.
2. ГОСТ 11. 006- 74. Правила проверки согласия опытного распределения с теоретическим.
3. Шторм Р. Теория вероятностей. Математическая статистика. Статистический контроль качества. М.: Мир, 1970.
Случайной величины Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x):
Понятие плотность распределения вероятностей случайной величины Х для дискретной величины неприменима...
Условия приобретения статуса индивидуального предпринимателя. В соответствии с п. 1 ст. 23 ГК РФ гражданин вправе заниматься предпринимательской деятельностью без образования юридического лица с момента государственной регистрации в качестве индивидуального предпринимателя. Каковы же условия такой регистрации и...
Седалищно-прямокишечная ямка Седалищно-прямокишечная (анальная) ямка, fossa ischiorectalis (ischioanalis) – это парное углубление в области промежности, находящееся по бокам от конечного отдела прямой кишки и седалищных бугров, заполненное жировой клетчаткой, сосудами, нервами и...
в виде последовательности интервалов 
и соответствующих им частот 
, причем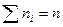 
(объем выборки). Требуется, используя критерий Пирсона, проверить гипотезу о том, что случайная величина X распределена равномерно.
и 
- концы интервала, в котором наблюдались возможные значения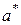 
и 
обозначены оценки параметров)
.
.
.
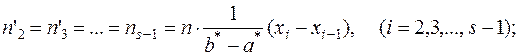
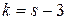, где 
- число интервалов, на которые разбита выборка.
и 
равномерного распределения по формулам: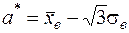 
, 
и выборочного среднего квадратического отклонения 
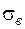примем середины 
интервалов в качестве вариант (наблюдаемых значений X). В итоге получим эмпирическое распределение равноотстоящих вариант:
.
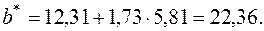
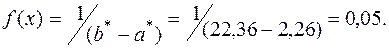
. Для этого составим таблицу.
. Так как 
< 
нет оснований отвергать гипотезу о равномерном распределении. Данные наблюдений согласуются с этой гипотезой.
, если имеется 20 опытных данных?
