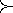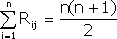Метод простого ранжирования.

Метод представляет собой процедуру упорядочения объектов, выполняемую экспертом. На основе знаний и опыта эксперт располагает объекты в порядке предпочтения, руководствуясь одним или несколькими выбранными показателями сравнения. В зависимости от вида отношений между объектами возможны различные варианты упорядочения объектов.

Рассмотрим эти варианты. Пусть среди объектов нет одинаковых по сравниваемым показателям, т.е. нет эквивалентных объектов. В этом случае между объектами существует только отношение строгого порядка. В результате сравнения всех факторов (объектов) по отношению строгого порядка составляется упорядоченная последовательность а₁ а₂ ... a_n, где объект с первым номером является наиболее предпочтительным из всех объектов, объект со вторым номером менее предпочтителен, чем первый объект, но предпочтительнее всех остальных объектов и т.д. Полученная система объектов с отношением строгого порядка при условии сравнимости всех объектов по этому отношению образует полный строгий порядок. Для этого отношения доказано существование числовой системы, элементами которой являются действительные числа, связанные между собой отношением неравенства >. Это означает, что упорядочению объектов соответствует упорядочение чисел х1 >... > xN, где х1=р (a₁).

Возможна и обратная последовательность х₁ <... < x_N, в которой наиболее предпочтительному объекту приписывается наименьшее число и по мере убывания предпочтения объектам приписываются большие числа.

Соответствие перечисленных последовательностей, т.е. их гомоморфизм, можно осуществить, выбирая любые числовые представления. Единственным ограничением является монотонность преобразования. Следовательно, допустимое преобразование при переходе от одного числового представления к другому должно обладать свойством монотонности. Таким свойством допустимого преобразования обладает шкала порядков, поэтому ранжирование объектов есть измерение в порядковой шкале.

В практике ранжирования чаще всего применяется числовое представление последовательности в виде натуральных чисел:

x1=φ(a1), x2=φ(a2), … xn=φ(an)

т.е. используется числовая последовательность. Числа х₁, х₂,...x_n в этом случае называются рангами и обычно обозначаются буквами г₁, r₂,... r_n.Применение строгих численных отношений «больше» (>), «меньше» (<) или «равно» (=) не всегда позволяет установить порядок между объектами. Поэтому наряду с ними используются отношения для определения большей или меньшей степени какого-то качественного признака (отношения частичного порядка, например, полезности), отношения типа «более предпочтительно» ( ), «менее предпочтительно» ( ), «равноценно» ( ) или «безразлично» (~). Упорядочение объектов при этом может иметь, например, следующий вид:

a1 a2 a3 ≈ a4 ≈ a5 a6 … an-1 ≈ an

Такое упорядочение образует нестрогий линейный порядок. Для отношения нестрогого линейного порядка доказано существование числовой системы с отношениями неравенства и равенства между числами, описывающими свойства объектов. Любые две числовые системы для нестрогого линейного порядка связаны между собой монотонным преобразованием. Следовательно, ранжирование при условии наличия эквивалентных объектов представляет собой измерение также в порядковой шкале.

В практике ранжирования объектов, между которыми допускаются отношения как строгого порядка, так и эквивалентности, числовое представление выбирается следующим образом.

Наиболее предпочтительному объекту присваивается ранг, равный единице, второму по предпочтительности - ранг, равный двум, и т.д. Для эквивалентных объектов удобно с точки зрения технологии последующей обработки экспертных оценок назначать одинаковые ранги, равные среднеарифметическому значению рангов, присваиваемых одинаковым объектам. Такие ранги называют связанными рангами.

Связанные ранги могут оказаться дробными числами. Удобство использования связанных рангов заключается в том, что сумма рангов n объектов равна сумме натуральных чисел от единицы до n. При этом любые комбинации связанных рангов не изменяют эту сумму. Данное обстоятельство существенно упрощает обработку результатов ранжирования при групповой экспертной оценке.

В общем случае, если, например, не удается различать факторы, занимающие места с р по q (область безразличия), то им всем присваивается ранг:

 

(фактически связанный ранг – это связанный ранг для данного промежутка). Для приведенного примера упорядочения на основе нестрогого линейного порядка при n = 10 ранги объектов а₃, а₄, а₅ будут равными г₃ = г₄ = г₅ = (3+4+5) / 3 = 4. В этом же примере ранги объектов а₉, и а₁₀ также одинаковы и равны среднеарифметическому г₉ = г10 = (9+10) / 2 = 9,5.

Существенно, что сумма всех рангов для данного эксперта должна быть постоянной и равняться .

Результатом опроса в случае метода ранжирования является матрица R= Rij, i=1...n, j= l...m, для j= 1,..., m:

Пример ЭМ- 1:

Пусть n = 5, m = 4, i=1...5, j = 1...4, тогда матрица R= (Rij) может иметь вид, приведенный в Таблица 0‑1

Таблица 0‑1