Задача 8.3.
1.Выборку значений СВ Х, указанную в условии задачи 8.1 сгруппировать, разбивая отрезок [a,b] (а = min хi; b = max хi) на 5 интервалов
и подсчитать частоты интервалов. 2. Предполагая, что Х распределена по нормальному закону и принимая в качестве параметров М[X], s[X] их оценки 3. С помощью критерия согласия Пирсона при уровне значимости α =0.1 проверить, согласуются ли выборочные данные с гипотезой о нормальном распределении величины Х. Число степеней свободы принять равным трём. Решение. 1. Из статистического ряда задачи 8.1видно, что а=min xi = 2, в = max xi = =10, поэтому (в-а)/5=1.6 и границы интервалов будут ξ0 = 2, ξ1 = 2+1.6=3.6, ξ2 = =3.6+1.6=5.2, ξ3 = 5.2+1.6=6.8, ξ4 = 6.8+1.6= 8.4, ξ5 = 8.4+1.6=10. Эмпирическая частота rj интервала 2. Примем в качестве параметров нормального распределения Х вычисленные в задаче8.1 значения точечных оценок M[X] = Теоретические частоты
С помощью таблиц интеграла Лапласа находим
3. Вычисляем значение
По таблице распределения χ2 Пирсона для доверительной вероятности g = 1-α = 0.9 и числа степеней свободы n = 3 находим значение
|

 с границами
с границами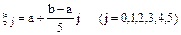
 , s вычислить теоретические частоты интерва-лов.
, s вычислить теоретические частоты интерва-лов. = 6.23, s[X] = s = 2.06
= 6.23, s[X] = s = 2.06 интервалов
интервалов 


 . Поскольку
. Поскольку 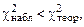 гипотезу о нормальном распределении СВ Х следует считать не противоречащей выборочным данным.
гипотезу о нормальном распределении СВ Х следует считать не противоречащей выборочным данным.


