Задание 7.5.
Найти вероятность попадания в заданный интервал [a,b] значения нормально распределенной случайной величины X, если известно её математическое ожидание M[X] и дисперсия D[X].
| Вар.
| M [ X ]
| D [ X ]
| 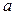
| b
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
| -2
|
| |
|
|
| -1
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
| -1
|
| |
| -8
|
| -9
|
| |
|
|
| -2
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
| -1
|
| |
|
|
|
|
|
Задание 7.6.
В партии из n изделий каждое может оказаться стандартным с вероятностью p. С помощью локальной и интегральной формул Муавра-Лапласа вычислить вероятность того, что число стандартных деталей в партии будет: а) равно m; б) заключено между m1 и m2.
| Вар.
| p
| n
| m
| m1
| m2
| |
| 0.3
|
|
|
|
| |
| 0,7
|
|
|
|
| |
| 0,5
|
|
|
|
| |
| 0,4
|
|
|
|
| |
| 0,6
|
|
|
|
| |
| 0,2
|
|
|
|
| |
| 0,4
|
|
|
|
| |
| 0,6
|
|
|
|
| |
| 0,3
|
|
|
|
| |
| 0,8
|
|
|
|
| |
| 0,3
|
|
|
|
| |
| 0,7
|
|
|
|
| |
| 0,2
|
|
|
|
| |
| 0,1
|
|
|
|
| |
| 0,5
|
|
|
|
| |
| 0,4
|
|
|
|
| |
| 0,6
|
|
|
|
| |
| 0,2
|
|
|
|
| |
| 0,3
|
|
|
|
| |
| 0,1
|
|
|
|
| |
| 0,7
|
|
|
|
| |
| 0,5
|
|
|
|
| |
| 0,6
|
|
|
|
| |
| 0,8
|
|
|
|
| |
| 0,1
|
|
|
|
| |
| 0,3
|
|
|
|
| |
| 0,2
|
|
|
|
| |
| 0,4
|
|
|
|
| |
| 0,6
|
|
|
|
| |
| 0,5
|
|
|
|
|
Задание 7.7.
Двумерная случайная величина (X,Y) имеет плотность распределения
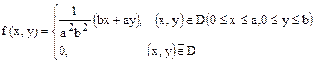
Найти вероятность попадания значения (X,Y) в область   вероятность попадания значения X в интервал вероятность попадания значения X в интервал  математическое ожидание M [ X ] и условное математическое ожидание математическое ожидание M [ X ] и условное математическое ожидание 
| Вар
| a
| b
| x1
| x2
| y1
| y2
| |
|
|
|
|
| -2
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
| -4
|
| |
|
|
| -4
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
| -2
|
| |
|
|
| -1
|
|
|
| |
|
|
| -3
|
|
|
| |
|
|
|
|
| -2
|
| |
|
|
|
|
| -1
|
| |
|
|
|
|
|
|
| |
|
|
| -2
|
|
|
| |
|
|
| -4
|
|
|
| |
|
|
|
|
| -3
|
| |
|
|
| -2
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
| -4
|
|
|
| |
|
|
|
|
| -4
|
| |
|
|
|
|
|
|
| |
|
|
| -2
|
|
|
| |
|
|
|
|
| -1
|
| |
|
|
|
|
| -3
|
| |
|
|
| -2
|
|
|
| |
|
|
| -1
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
| -2
|
| |
|
|
|
|
| -4
|
| |
|
|
| -3
|
|
|
|
Задание 7.8.
Случайная величина Х имеет плотность распределения f (x). Для случайной величины Y = j (X) найти плотность распределения g (y), вероятность P (a £ Y £ b), математическое ожидание M [ Y ] и дисперсию D [ Y ].
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
Задание 7.9.
Задана матрица перехода системы из состояния i (i =1,2) в состояние j (j =1,2) за один шаг  . Найти матрицу перехода из состояния i в состояние j за два шага. . Найти матрицу перехода из состояния i в состояние j за два шага.
| Вар.
| a
| b
| C
| D
| |
| 0,1
| 0,9
| 0,2
| 0,8
| |
| 0,2
| 0,8
| 0,7
| 0,3
| |
| 0,3
| 0,7
| 0,4
| 0,6
| |
| 0,4
| 0,6
| 0,5
| 0,5
| |
| 0,6
| 0,4
| 0,7
| 0,3
| |
| 0,6
| 0,4
| 0,8
| 0,2
| |
| 0,8
| 0,2
| 0,9
| 0,1
| |
| 0,8
| 0,2
| 0,2
| 0,8
| |
| 0,9
| 0,1
| 0,2
| 0,8
| |
| 0,4
| 0,6
| 0,1
| 0,9
| |
| 0,7
| 0,3
| 0,2
| 0,8
| |
| 0,5
| 0,5
| 0,4
| 0,6
| |
| 0,3
| 0,7
| 0,2
| 0,8
| |
| 0,2
| 0,8
| 0,5
| 0,5
| |
| 0,9
| 0,1
| 0,7
| 0,3
| |
| 0,9
| 0,1
| 0,8
| 0,2
| |
| 0,8
| 0,2
| 0,3
| 0,7
| |
| 0,4
| 0,6
| 0,3
| 0,7
| |
| 0,5
| 0,5
| 0,4
| 0,6
| |
| 0,3
| 0,7
| 0,6
| 0,4
| |
| 0,8
| 0,2
| 0,4
| 0,6
| |
| 0,2
| 0,8
| 0,5
| 0,5
| |
| 0,2
| 0,8
| 0,1
| 0,9
| |
| 0,4
| 0,6
| 0,7
| 0,3
| |
| 0,1
| 0,9
| 0,4
| 0,6
| |
| 0,2
| 0,8
| 0,7
| 0,3
| |
| 0,4
| 0,6
| 0,5
| 0,5
| |
| 0,2
| 0,8
| 0,2
| 0,8
| |
| 0,5
| 0,5
| 0,3
| 0,7
| |
| 0,7
| 0,3
| 0,9
| 0,1
|
Контрольная работа №8
"Математическая статистика";
Задание 8.1.
Из генеральной совокупности извлечена выборка, представленная в виде статистического ряда (в первой строке указаны выборочные значения, во второй - соответствующие им частоты). Требуется вычислить выборочное среднее, выборочную дисперсию DB, исправленную выборочную дисперсию s2 и среднеквадратическое отклонение s, эмпирическую функцию распределения.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
| xi
| 8,5
| 9,5
| 10,5
| 11,5
| 12,5
| 13,5
| 14,5
| | ni
|
|
|
|
|
|
|
| 13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
Задание 8.2.
По заданным выборочным среднему и исправленному среднеквадратическому отклонению s найти с доверительной вероятностью p доверительный интервал для математического ожидания M[X], если
а)  известно (принять известно (принять  ), ),
б)  неизвестно, неизвестно,

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
|
Примеры решения типовых задач. Пример 1.Степень диссоциации уксусной кислоты в 0,1 М растворе равна 1,32∙10-2
Пример 1.Степень диссоциации уксусной кислоты в 0,1 М растворе равна 1,32∙10-2. Найдите константу диссоциации кислоты и значение рК.
Решение. Подставим данные задачи в уравнение закона разбавления
К = a2См/(1 –a) =...
Экспертная оценка как метод психологического исследования Экспертная оценка – диагностический метод измерения, с помощью которого качественные особенности психических явлений получают свое числовое выражение в форме количественных оценок...
В теории государства и права выделяют два пути возникновения государства: восточный и западный Восточный путь возникновения государства представляет собой плавный переход, перерастание первобытного общества в государство...
|
ПРОФЕССИОНАЛЬНОЕ САМОВОСПИТАНИЕ И САМООБРАЗОВАНИЕ ПЕДАГОГА Воспитывать сегодня подрастающее поколение на современном уровне требований общества нельзя без постоянного обновления и обогащения своего профессионального педагогического потенциала...
Эффективность управления. Общие понятия о сущности и критериях эффективности. Эффективность управления – это экономическая категория, отражающая вклад управленческой деятельности в конечный результат работы организации...
Мотивационная сфера личности, ее структура. Потребности и мотивы. Потребности и мотивы, их роль в организации деятельности...
|
|

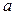
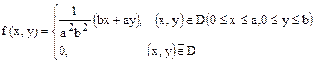

 вероятность попадания значения X в интервал
вероятность попадания значения X в интервал 






























 . Найти матрицу перехода из состояния i в состояние j за два шага.
. Найти матрицу перехода из состояния i в состояние j за два шага. известно (принять
известно (принять  ),
),


