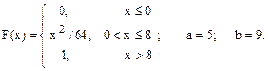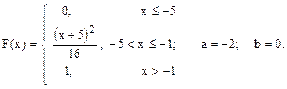Задание 7.3.

Построить ряд распределения, функцию распределения и ее график, найти математическое ожидание и дисперсию случайной величины X - числа наступлений случайного события А в указанной ниже серии независимых испытаний.

 

1. Монета подбрасывается 4 раза. А - выпадение герба при одном бросании, Р(А)=0,5.

2. Стрелок стреляет по мишени 3 раза. А - попадание при одном выстреле, Р(А)=0,6.

3. Рыболов трижды забрасывает удочку. А - поклевка при одном забрасывании, Р(А)=0,3.

4. Из урны, содержащей 2 белых и 3 черных шара, извлекается наугад шар (если он белый, то наступило А), который затем возвращается в урну. Опыт повторяется 3 раза.

5. Высеиваются 3 семечка тыквы. Всхожесть (вероятность всхода А одного семени) равна Р(А)=0,8.

6. Элементарная частица может быть зарегистрирована прибором (событие А) с вероятностью Р(А)=0,7. Перед прибором поочередно пролетают три частицы.

7. А -событие, наступающее, когда первая цифра номера встречного автомобиля - нуль. Мимо поочередно проезжают два автомобиля.

8. А - выход из строя электрооборудования автомобиля в течение года, Р(А)=0,3. Рассматриваются три автомобиля.

9. А - событие, состоящее в побитии мирового рекорда спортсменом, Р(А)=0,2. В соревновании участвуют три спортсмена.

10. Орудие выпускает по цели три снаряда. А - попадание снаряда, Р(А)=0,8.

11. Извлеченная наугад с книжной полки книга может оказаться учебником (событие А) с вероятностью Р(А)=0,4. Извлекается три книги.

12. Позитрон при рождении может приобрести правую (событие А) или левую ориентацию вращения, Р(А)=0,6. Рассматриваются 3 позитрона.

13. Наличие синей глины указывает на возможность алмазного месторождения (событие А) с вероятностью Р(А)=0,4. Синяя глина обнаружена в трех районах.

14. В период цветения растение может быть опылено (событие А) с вероятностью Р(А)=0,8. Рассматриваются 4 растения.

15. Рыболов может поймать рыбу при поклевке (событие А) с вероятностью Р(А)=0,4. У рыболова было три поклевки.

16. В ядерной реакции может образоваться резонансная частица (событие А) с вероятностью Р(А)=0,2. Рассматриваются три реакции.

17. Помещенный в грунт саженец может приняться (событие А) с вероятностью Р(А)=0,7. Высажено три саженца.

18. Генератор электростанции в течение года может выйти из строя (событие А) с вероятностью Р(А)=0,2. Рассматривается трехлетний период эксплуатации генератора.

19. В течение суток молоко в горшке может прокиснуть (событие А) с вероятностью Р(А)=0,4. Рассматривается случай трех горшков.

20. На фотографии, полученной в камере Вильсона частица регистрируется в опыте (событие А) с вероятностью Р(А)=0,5. Проведено 4 опыта.

21. А - появление четного числа очков при бросании игральной кости. Кость выбрасывается 4 раза.

22. Три орудия стреляют по своим целям, А - попадание снаряда в цель, Р(А)=0,7.

23. Рыболов при поклевке может вытащить рыбу (событие А) с вероятностью Р(А)=0,6. Поклевка произошла у 4 рыболовов.

24. Биение ротора электродвигателя приводит к его выходу из строя в вероятностью Р(А)=0,8. Рассматриваются три однотипных двигателя.

25. При изготовлении детали она может оказаться бракованной (событие А) с вероятностью Р(А)=0,2. Изготовлено три детали.

26. Станок работает безотказно в течение года (событие А) с вероятностью Р(А)=0,8. В цехе работают 4 станка.

27. А - появление нечетного числа очков при бросании игральной кости. Кость выбрасывается 4 раза.

28. Поезд может прибыть по расписанию (событие А) с вероятностью Р(А)=0,9. Рассматриваются три рейса.

29. В среднем при наборе страницы текста оператор совершает ошибку (событие А) в 30% случаев. Статья содержит 4 страницы текста.

30. Самолет-разведчик может обнаружить цель (событие А) с вероятностью Р(А)=0,8. Для обнаружения цели послано три самолета.

Задание 7.4.

По заданной функции распределения F(x) случайной величины СВ X найти плотность распределения и построить ее график. Вычислить вероятность P(a≤X≤b) попадания значения СВ в заданный интервал, математическое ожидание и дисперсию.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.