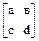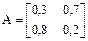Контрольной работы № 7
Задание 7.1. Для доставки экстренного сообщения отправлены различными маршрутами два курьера. Вероятности своевременной доставки сообщения курьерами равны 0,8 и 0,6 соответственно. Найти вероятности того, что: а) своевременно успеют оба курьера; б) только один курьер; в) хотя бы один курьер; г) оба курьера опоздают.
Решение. Обозначим через A, B случайные события, наступающие в случаях, когда успевают первый или второй курьеры соответственно, р(А)=0,8, р(В)=0,6. Введем также события: С - успевают оба курьера, D - только один курьер, Е - хотя бы один курьер, F - оба курьера опоздают. а) Представим событие в виде С=А·В. Применяя теорему умножения вероятностей и учитывая очевидную из условия независимость событий А, В находим Р(С) = Р(А · В) = Р(А) · Р(В) = 0,8 · 0,6 б) Согласно условию D=А· Р(D) = P(А·
Вновь применяя теорему умножения при независимых сомножителях находим P(D) = P(A)·P( = 0,8(1-0,6) + (1-0,8) = 0,28. в) Здесь D = A + B. Слагаемые А, В совместны, поэтому теорема сложения запишется P(D) = P(A+B) = P(A) + P(B) - P(A·B) = P(A) + (B) - P(A) · P(B) = 0,8+0,6-0,8·0,6 = 0,92. г) По условию F = Заметим также, что события D + F является достоверным, поэтому P(D + F) = 1. Поскольку D, F несовместны, то P(D + F) = P(D) + P(F), откуда можно также найти вероятность P(F) = 1- P(D) = 0,08.
Задание 7.2. На сборку телевизоров поступают однотипные кинескопы от двух заводов, поставляющих соответственно 60% и 40% кинескопов. Вероятность для кинескопа оказаться нестандартным равна: 0,1 - на первом заводе, 0,2 - на втором. Найти вероятность того, что: а) очередной на сборке кинескоп будет нестандартным; б) оказавшийся нестандартным кинескоп изготовлен вторым заводом.
Решение. Обозначим через Нi (i = 1,2) гипотезу - кинескоп изготовлен i-тым заводом. Очевидно, что Н1, Н2 несовместны и Н1 + Н2 = I - достоверное событие. Из условия видно также, что Р(Н1) = 0,6, Р(Н2) = 0,4. Обозначим через А событие: очередной кинескоп окажется нестандартным. а) По формуле полной вероятности имеем: Р(А) = Р(А / Н1) · Р(Н1) + Р(А / Н2) · Р(Н2). Согласно условию Р(А / Н1) = 0,1, Р(А / Н2) = 0,2, поэтому Р(А) = 0,1·0,6 + 0,2·0,4 = 0,14. б) Для вычисления искомой вероятности Р(Н2 / А) используем формулу Байеса
Задание 7.3. Построить ряд распределения, функцию распределения и её график, и найти математическое ожидание и дисперсию случайной величины Х - числа наступлений случайного события А в указанный ниже серии независимых испытаний: поступила партия из 3 изделий, каждое из которых может оказаться бракованным (событие А, Р(А) = 0,4).
Решение. Случайная величина (СВ)Х - число бракованных изделий - может принимать значения 0, 1, 2, 3. Вероятности этих значений вычисляются по формуле Бернулли при р = 0,4, q = 1- 0,4 = 0,6.
Ряд распределения СВ Х имеет вид:
Функция распределения по определению равна F(x) = P(X < x) и запишется:
График показан на рисунке.
x
1 2 3
Вычисляем математическое ожидание и дисперсию:
D[ x ] = 2,16 - (1,2)2 = 0,72.
Задание 7.4. По заданной функции распределения F(x) CB X найти плотность распределения и построить её график. Вычислить вероятность Р(а ≤ Х ≤ в) попадания значения СВ в заданный интервал, математическое ожидание и дисперсию.
а = -3; в = 5.
Решение. Плотность распределения определяется по формуле
и показана на рисунке
0 2 6 x
Искомая вероятность равна: Математическое ожидание и дисперсия запишутся:
Задание 7.5. Найти вероятность попадания в заданный интервал значения нормаль- ного распределённой СВ Х, если известно её математическое ожидание М[ x ] и дис- персия D[x]. M[ x ] = 4; D[ x ] = 25; a = -7; в = 9.
Решение. Искомая вероятность вычисляется по формуле
Среднеквадратическое отклонение
Здесь учтена нечётность вспомогательной функции Берём её значение из таблицы: Ф(1) =, Ф(2,2) =, откуда Р =.
Задание 7.6. В партии из n деталей каждая может оказаться стандартной с вероятностью р. С помощью локальной и интегральной формул Муавра-Лапласа вычислить вероятность того, что число стандартных деталей в партии будет: а) равно m; б) заключено между m 1 и m 2. p =0,4; n = 350; m = 146; m 1 = 135; m 2 = 152.
Решение. а) Искомая вероятность при n >> 1, np >> 1 вычисляется по локальной формуле (q = 1 - p)
где вспомогательная функция имеет вид: Для х = 0,66 имеем после вычислений р1 = 0,03.
б) Вероятность вычисляется с помощью интегральной формулы
откуда с помощью таблицы для Ф(х) и имеем Р2 = + =
Задание 7.7. Двумерная случайная величина (X,Y) имеет плотность распределения
Найти вероятность попаданий значения (X,Y) в область х 1 ≤ х ≤ х 2, y 1 ≤ y ≤ y 2, вероятность попадания значения Х в интервал х 1 ≤ х ≤ х 2, математическое ожидание М[ x ] и условное математическое ожидание M[Y/X = x ]. a = 2, в = 5, х 1 = 1, х 2 = 9, у 1 = - 4, у 2 = 3.
Решение. Найдём вероятность попадания в область S(х 1 ≤ х ≤ х 2, y 1 ≤ y ≤ y 2) по формуле Р(х 1 ≤ X ≤ х 2, y 1 ≤ Y ≤ y 2) = При вычислении интеграла учитывается та часть области S, где f ≠ 0, т.е. 1 ≤ х ≤ 2, 0 ≤ у ≤ 3:
Плотность вероятности для составляющей Х имеет вид: Если х < 0 или х > 2, то f (x, y) = 0 и f 1(x) = 0. При 0 ≤ х ≤ 2 находим
Таким образом плотность имеет вид:
Тогда
Условное математическое ожидание М[Y/X = x ] определяется с помощью услов-ной плотности распределения f 2(y / x) составляющей Y (т.е. плотности СВ Y при условии, что СВ Х приняла известное значение х):
Согласно (1) СВ Х может принимать лишь значения 0 ≤ х ≤ 2, поэтому из (2), (1) и условия задачи получаем
Искомое математическое ожидание равно
Полученная зависимость называется уравнением регрессии Y на Х.
Задание 7.8. СВ Х имеет плотность распределения. Для СВ Y = φ(Х) найти её плотность распределения g (y), вероятность P(а ≤ Y ≤ в), математическое ожидание M[Y] и дисперсию D[Y].
Решение. Плотность распределения СВ Y = φ(x) даётся формулой
g (y) = f (ψ(y))/ψ'(y)/ (1)
где х = ψ(у) - функция, обратная к у = φ(х). В данном случае у = φ(х) = 2 х - 3, х = ψ(у) = (у + 3)/2. Согласно и условию задачи находим
Остальные величины можно вычислить с помощью g (y) или непосредственно через f (x) по формулам
Задание 7.9. Задана матрица перехода системы из состояния i (i = 1, 2) в состояние j (j = 1, 2) за один шаг:
Найти матрицу перехода из состояния i в состояние j за два шага. а = 0,3, в = 0,7, с = 0,8, d = 0,2
Решение. Заданная матрица имеет вид:
Матрица перехода i → j за n шагов равна Аn и для n = 2 запишется
Решение типового варианта
|

 +
+  ·В (чертой обозначены противоположные события). По теореме сложения вероятностей с учетом несовместности слагаемых имеем
·В (чертой обозначены противоположные события). По теореме сложения вероятностей с учетом несовместности слагаемых имеем +
+ 
 ,
,  ,
, ,
, 
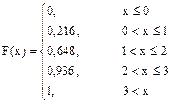
 F(x)
F(x)










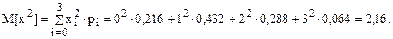


 f (x)
f (x)

 0,75
0,75






 поэтому
поэтому


 .
.


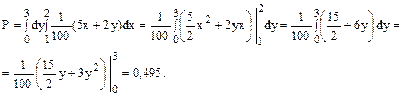
 .
.
 (1)
(1)

 (2)
(2)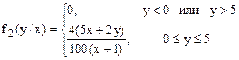
 (3)
(3)