По заданной корреляционной таблице найти выборочные средние 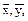 среднеквадратические отклонения sΧ, sΥ, коэффициент корреляции ρΧΥ и уравнение линейной регрессии Y на X. Вычислить условные средние
среднеквадратические отклонения sΧ, sΥ, коэффициент корреляции ρΧΥ и уравнение линейной регрессии Y на X. Вычислить условные средние 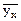 по дан-ным таблицы и найти наибольшее их отклонение от значений, вычисляемых из уравнения регрессии.
по дан-ным таблицы и найти наибольшее их отклонение от значений, вычисляемых из уравнения регрессии.
Решение. Вычислим выборочные средние и среднеквадратические отклонения для X,Y


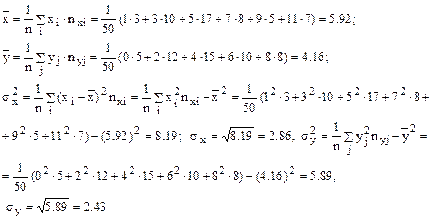
Выборочный коэффициент корреляции между Х и У отыскивается по формуле
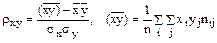
Согласно таблице
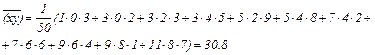
откуда

Выборочное линейное уравнение регрессии У на Х имеет вид
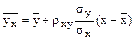
или, с учётом вычисленных значений,
 (1)
(1)
Условное среднее при x = xi вычисляется по формуле
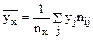
где 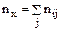 - число выборочных значений yj , наблюдавшихся при данном x i. Согласно данным из таблицы находим
- число выборочных значений yj , наблюдавшихся при данном x i. Согласно данным из таблицы находим
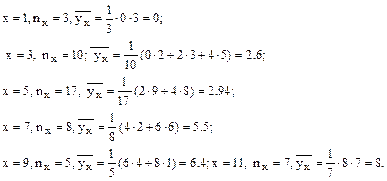 2)
2)
Значения условных средних 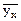 , отыскиваемые по уравнению регрессии (1):
, отыскиваемые по уравнению регрессии (1):
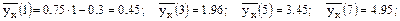


Отклонения значений (2), (3)  будут
будут
d1 = 0-0.45=-0.45; d2 = 2.6- 1.96 = 0.65; d3 = -0.51, d4 = 0.55; d5 = -0.05;
d6 = 0.05.
Наибольшее по абсолютной величине отклонение равно 0.65.
С о д е р ж а н и е
| 1.
| Контрольные работы.....................................
|
|
|
| 1.1.
| Правила оформления контрольных работ....................
|
|
|
| 1.2.
| Выбор варианта контрольной работы........................
|
|
|
| 1.3.
| Задания контрольных работ.................................
|
|
|
| К о н т р о л ь н а я р а б о т а № 5..............................
|
|
|
| К о н т р о л ь н а я р а б о т а № 6..............................
|
|
|
| К о н т р о л ь н а я р а б о т а № 7..............................
|
|
|
| К о н т р о л ь н а я р а б о т а № 8..............................
|
|
| 2.
| Примеры решения задач контрольных работ.......
|
|
|
| 2.1.
| Решение типового варианта контрольной работы № 1.........
|
|
|
| 2.2.
| Решение типового варианта контрольной работы № 2.........
|
|
|
| 2.3.
| Решение типового варианта контрольной работы № 3.........
|
|
|
| 2.4.
| Решение типового варианта контрольной работы № 4.........
|
|
Учебное издание
Высшая математика
Программа, методические указания и контрольные задания
для студентов-заочников инженерных и
инженерно-экономических специальностей
приборостроительного факультета
В 2-х частях
Ч а с т ь II
Составители: ИБРАГИМОВ Владислав Ахмедович
СТРЕЛЬЦОВ Сергей Викторович
МЕЛЕШКО Алексей Николаевич
БОКУТЬ Людмила Валентиновна

 среднеквадратические отклонения sΧ, sΥ, коэффициент корреляции ρΧΥ и уравнение линейной регрессии Y на X. Вычислить условные средние
среднеквадратические отклонения sΧ, sΥ, коэффициент корреляции ρΧΥ и уравнение линейной регрессии Y на X. Вычислить условные средние 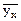 по дан-ным таблицы и найти наибольшее их отклонение от значений, вычисляемых из уравнения регрессии.
по дан-ным таблицы и найти наибольшее их отклонение от значений, вычисляемых из уравнения регрессии.
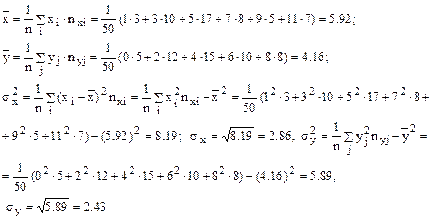
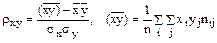
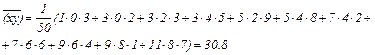

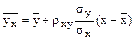
 (1)
(1)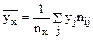
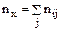 - число выборочных значений yj , наблюдавшихся при данном x i. Согласно данным из таблицы находим
- число выборочных значений yj , наблюдавшихся при данном x i. Согласно данным из таблицы находим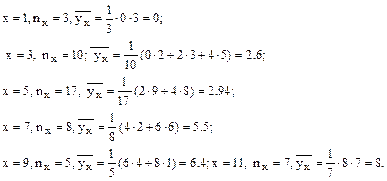 2)
2)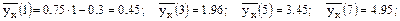


 будут
будут


