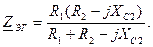Методические указания по выполнению задачи 2
1. Проработать материал, изложенный в [1,т.1. §4.1-4.10,§5.1-5.24,§6.1-6.9]. 2. Расчет линейных электрических схем синусоидального тока аналогичен расчету схем постоянного тока. Для схем постоянного тока уравнения составляют по действительным значениям напряжений, токов, сопротивлений и проводимостей. В схемах же синусоидального тока для алгебраизации интегродифференциальных уравнений применяют комплексные (символические) величины:
При этом все параметры записывают в виде комплексных чисел в алгебраической, показательной или тригонометрической форме. При переходе от интегродифференциальных уравнений дифференцирование мгновенного значения заменяют умножением jw на соответствующую комплексную величину, а интегрирование - делением комплексной величины на jw.
если Изображение синусоидальных функций времени комплексными величинами позволяет использовать для расчета цепей переменного тока методы расчета цепей постоянного тока: уравнения Кирхгофа и Ома, метод эквивалентных преобразований, метод контурных токов, метод узловых потенциалов, метод наложения, метод эквивалентного генератора и т.д. 3. При составлении системы уравнений по законам Кирхгофа руководствоваться следующим. Заданная схема (рис. 1.2) содержит два узла и три ветви. Значит всего уравнений должно быть три, из них по первому закону Кирхгофа - одно и по второму -два. Для выбранных направлений токов и обходов контуров (рис. 1.2) система уравнений в дифференциальной форме имеет вид: узел а: контур 1
контур 2  . .
Уравнения в символической форме: узел а: контур 1 контур 2 4. Система уравнений по методу контурных токов. Определяется количество независимых контуров (nв-nу+1). Для схемы на рис.1.2 выбираются два независимых контура и задается направление контурных токов в них Система расчетных уравнений имеет вид:
где
Согласно выбранным направлениям токов (в ветвях и контурных токов), токи ветвей определяются уравнениями
5. В схеме (рис. 1.2) всего один независимый узел, поэтому по методу узловых потенциалов составляется одно уравнение (принимаем где
Токи в ветвях через потенциалы узлов определяются уравнениями
6. Для расчета токов в ветвях (рис. 1.2) можно воспользоваться методом узловых потенциалов, как наиболее оптимальным (меньшее число расчетных уравнений). Параметры цепи (рис. 1.2): Rl = R2 = R3 = ХС2 = XL3 = 5 Ом; действующие значения Э.Д.С.: Е1 = 4,47 В; ЕЗ = 8 В; начальные фазы φ: φ1=63;40; φ3=00. Комплексы Э.Д.С:
Правильность расчетов можно проверить по первому закону Кирхгофа. İ;1- İ;2- İ;3=0; -0.2+ j 0.8-0.3- j 0.3+0.5- j 0.5=0, Законы изменения токов в ветвях в функции времени
Соответствующие им графики представлены на рис. 1.3. 7. Топографическую диаграмму для электрической схемы строят, откладывая на комплексной плоскости векторы комплексных потенциалов для всех точек схемы. Разность потенциалов (напряжение) между двумя любыми точками схемы, например, между точками а и b Алгоритм построения топографической диаграммы. 7.1. Обозначают точки схемы (буквами или цифрами); потенциал какой-либо точки схемы принимают за нулевой (заземляют). 7.2. По найденным токам и параметрам схемы вычисляют потенциалы обозначенных точек схемы при обходе каждой ветви, начиная с точки нулевого потенциала. Если направление обхода пассивного элемента схемы совпадает с направлением тока, протекающего по этому элементу, то потенциал уменьшается на величину напряжения на элементе. 7.3. Выбирают масштабы для токов mI (мм/А) и напряжений mU (мм/В). 7.4. Строят векторную диаграмму токов, откладывая их на комплексной плоскости из начала координат в выбранном масштабе. 7.5. Строят комплексные потенциалы в масштабе и полученные точки соединяют в той же последовательности как они определялись. 7.6. Рассмотрим построение векторной диаграммы токов и топографической диаграммы напряжений для схемы на рис. 1.2. Пусть

При правильном расчете топографической диаграммы потенциалы точки а, найденные при обходе разных ветвей, должны совпадать. Векторная диаграмма токов и топографическая диаграмма напряжений, построенные в масштабе по результатам расчета заданной схемы (рис. 1.2) даны на рис. 1.4. 8. Полагая в качестве нагрузки последовательное соединение элементов цепи R3 и L3 определим параметры эквивалентного генератора В режиме холостого хода (İ3 = 0)

Внутреннее сопротивление эквивалентного генератора

9. При составлении уравнений по законам Кирхгофа с учетом взаимоиндукции между катушками необходимо выяснить как включены эти катушки (согласно или встречно). Катушки считаются включенными согласно, если направление токов в них ориентировано одинаково относительно однополярных зажимов катушек.

Для схемы на рис.1.6 направление токов I1 и I2 ориентировано по разному относительно однополярных зажимов (в катушке L1 ток направлен от начала катушки к ее концу, а в катушке L2 — наоборот), то есть катушки L1 и L2 включены встречно. Следовательно, напряжение взаимоиндукции будет вычитаться из напряжения самоиндукции, и напряжения на катушках L1 и L2 определяются выражениями
или в символической форме
10. Для выполнения п.10 необходимо для ряда значений изменяемого параметра провести расчет токов любым методом. Идеальным вариантом в данном случае является применение ЦВМ. 11. Сделать выводы по работе.
|





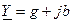 .
.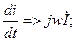
 ,
,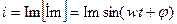 .
.



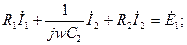
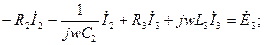
 ,
,  (рис. 1.2).
(рис. 1.2).
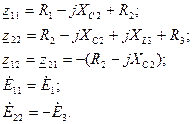







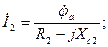
 .
.


 , определяется на диаграмме вектором, проведенным из точки b в точку а. Стрелка вектора указывает направление возрастания потенциала.
, определяется на диаграмме вектором, проведенным из точки b в точку а. Стрелка вектора указывает направление возрастания потенциала.
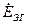 ,
,  (рис. 1.5). Э.Д.С. эквивалентного генератора
(рис. 1.5). Э.Д.С. эквивалентного генератора  в режиме холостого хода
в режиме холостого хода  , т.е.
, т.е. 
 .
. является входным сопротивлением схемы (рис. 1.5) относительно зажимов а и b при İ3 = 0.
является входным сопротивлением схемы (рис. 1.5) относительно зажимов а и b при İ3 = 0.