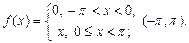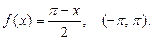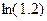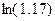| 1)
| 
|
| 2)
| 
|
| 3)
| 
|
| 4)
| 
|
| 5)
| 
|
| 6)
| 
|
| 7)
| 
|
| 8)
| 
|
| 9)
| 
|
|
|
|
| 10)
| 
|
|
|
|
Разложить данную функцию f(x) в ряд Фурье в интервале (a, b).
| 1)
| 
|
| 2)
| 
|
| 3)
| 
|
| 4)
| 
|
| 5)
| 
|
| 6)
| 
|
| 7)
| 
| 8)
| 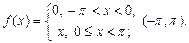
|
| 9)
| 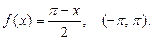
|
|
|
|
| 10)
| 
|
|
№ 4. Вычислить приближенно значения выражений, используя ряды:
| 1)
| 
|
| 2)
| 
|
| 3)
| 
|
| 4)
| 
|
| 5)
| 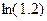
|
| 6)
| 
|
| 7)
| 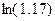
|
| 8)
| 
|
| 9)
| 
|
| 10)
| 
|
Числовые значения a, b, c, d для следующих трех примеров берутся по номеру варианта из приведенной ниже таблицы:
№ 5. В ящике а деталей, из них b бракованных. Сборщик наугад берет с деталей. Какова вероятность того, что а) все взятые детали – бракованные? б) среди взятых деталей только d бракованных?
№ 6. Испытывается каждый из а элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0.9. Найти наивероятнейшее число отказавших элементов и вероятность этого числа элементов.
№ 7. Задана дискретная случайная величина Х. Найти ее математическое ожидание и дисперсию. Построить график функции распределения.
| Х
| d
| c
| b
| a
|
| Р
| 0.2
| 0.1
| 0.3
| 0.4
|
Для приведенной ниже выборки из 50 элементов построить дискретный вариационный ряд, найти моду, медиану и среднее. Построить полигон.
| Вар. 1
| Вар. 2
| Вар. 3
| Вар. 4
| Вар. 5
| Вар. 6
| Вар. 7
| Вар. 8
| Вар. 9
| Вар. 10
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построить интервальный вариационный ряд с равными промежутками (10-14, 14-18, …) для приведенной выборки из 50 элементов. Построить гистограмму.
| Вар. 1
| Вар. 2
| Вар. 3
| Вар. 4
| Вар. 5
| Вар. 6
| Вар. 7
| Вар. 8
| Вар. 9
| Вар. 10
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Только для специальностей КШИ, ТШИ, БРА). Проверить, будет ли векторное поле потенциальным и соленоидальным. В случае потенциальности поля найти его потенциал.
| № вар
| задание
| № вар
| задание
|
|
| 
|
| 
|
|
| 
|
| 
|
|
| 
|
| 
|
|
| 
|
| 
|
|
| 
|
| 
|