НЕКОТОРЫЕ ПРИМЕРЫ
ПРИМЕР 1. Исследовать на сходимость ряд
Решение. Сравним данный ряд с рядом Используем предельный признак сравнения.
Так как предел конечен и не равен 0, а ряд ПРИМЕР 2. Исследовать на сходимость ряд
Решение. Имеем
следовательно, по признаку Даламбера исходный ряд расходится. ПРИМЕР 3. Найти область сходимости функционального ряда
Решение. По признаку Коши (радикальному) имеем
При вычислении предела использован известный предел Итак, R =1, следовательно, данный ряд сходится, если Исследуем поведение ряда на концах интервала. Пусть ПРИМЕР 4. Найти область сходимости степенного ряда
Решение. Найдем область сходимости ряда, используя признак Даламбера.
Таким образом, ряд сходится при ПРИМЕР 5. Разложить функцию f (x)= x2 в ряд Фурье на интервале [-p,p]. Решение.
Тогда Окончательно получим ПРИМЕР 6. В ящике 13 деталей, из них 10 – бракованных. Наугад берут 5 деталей. Какова вероятность, того, что среди взятых деталей 3 бракованных? Решение. Событие А состоит в том, среди взятых деталей окажется 3 бракованных. P(A)= m/n. Сначала найдем количество всевозможных исходов n. Так как берем наугад 5 деталей из 13, без учета порядка, то ПРИМЕР 7. Всхожесть семян равна 70%. Какова вероятность того, что из 10 семян взойдут а) 8; b) по крайней мере 8? Решение. Событие А состоит в том, что семечко взойдет. По условию задачи, n =10, p =70%=0.7, q= 1 -p =0.3. а). По формуле Бернулли Р10(8) = С810* p 8* q 10-8 = = 45*(0.7)8*(0.3)2 = 0.2335. b) Р = Р10(8) + Р10(9) + Р10(10) = 45*(0.7)8*(0.3)2 +10*(0.7)9*(0.3)1 +(0.7)10=0.38. ПРИМЕР 8. Построить график функции распределения д.с.в., заданной законом распределения:
Решение. Если х £ 2, то F(x)=P(X< x)=0, т.к. нет значений с.в. Х, меньших 2. Если 2 < х £ 4, то F(x)=P(X< x)=P(x=2)=0.1. Если 4 < х £ 6, то F(x)=P(X< x)=P[(x =2)+(x =4)]=0.1+0.3=0.4. Если х > 6, то F(x)=P(X< x)=P[(x =2)+(x =4)+(x =6)]=1. График функции распределения будет выглядеть следующим образом:
ПРИМЕР 9. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины, заданной законом распределения:
Решение. Математическое ожидание М(Х)=0*0.72+1*0.26+2*0.02 = 0.3. Дисперсия D(X)=(0-0.3)2*0.72+(1-0.3)2*0.26+(2-0.3)2*0.02 = 0.25. Среднее квадратическое отклонение s (Х)=0.5.
|

 .
. этот ряд сходится, так как является обобщенным гармоническим,
этот ряд сходится, так как является обобщенным гармоническим,  .
.
 .
. сходится, то сходится и ряд
сходится, то сходится и ряд  .
.

 ,
,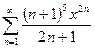 .
. .
. .
. .
. тогда имеем числовой ряд
тогда имеем числовой ряд  . Этот ряд расходится, так как
. Этот ряд расходится, так как  , т.е. не выполняется необходимое условие сходимости ряда. Итак,
, т.е. не выполняется необходимое условие сходимости ряда. Итак,  область сходимости ряда.
область сходимости ряда. .
. .
. . Исследуем сходимость ряда на границах. При
. Исследуем сходимость ряда на границах. При  имеем числовой ряд
имеем числовой ряд  , который расходится по необходимому признаку. При
, который расходится по необходимому признаку. При  получим знакочередующийся числовой ряд
получим знакочередующийся числовой ряд  , который также расходится по необходимому признаку. Итак,
, который также расходится по необходимому признаку. Итак,  , следовательно, функция f (x) – четная. Значит,
, следовательно, функция f (x) – четная. Значит,  . Кроме того, Т=p. Тогда по формуле,
. Кроме того, Т=p. Тогда по формуле,  .
.
 , или
, или  .
.
 . Теперь найдем число благоприятных исходов m. Так как три детали должны оказаться бракованными, то оставшиеся две детали должны быть качественными (т.е. взятыми из трех годных деталей, находящихся в ящике). Таким образом,
. Теперь найдем число благоприятных исходов m. Так как три детали должны оказаться бракованными, то оставшиеся две детали должны быть качественными (т.е. взятыми из трех годных деталей, находящихся в ящике). Таким образом,  . P(A)=360/1287=0,28.
. P(A)=360/1287=0,28.



