Определение коэффициента трения скольжения с помощью вращающегося диска.
Оборудование: проигрыватель с вращающемся диском, деревянное и металлическое тело небольших размеров, секундомер, линейка с миллиметровыми делениями.
Метод выполнения работы:
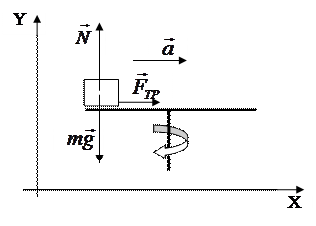
Тело, находящееся на вращающемся диске удерживается от проскальзывания силой трения покоя. Вращаясь по окружности оно испытывает центростремительное ускорение Видим, что ускорение прямо пропорционально радиусу окружности, а следовательно и силе трения покоя. Если увеличить радиус окружности, то сила трения покоя возрастает, но она может возрастать до определенного максимального значения, после чего трение покоя заменяется трением скольжения, и тело начинает скользить, улетая с диска. Таким образом, цель работы заключается в том, чтобы найти положение тела на диске, при котором трение покоя принимает максимально возможное значение и переходит в трение скольжения. Сила трения скольжения равна Подставим все полученные выражения во второй закон Ньютона. Получим
Порядок выполнения работы: 1. Включите проигрыватель на 78 об/мин и измерьте время t 15-20 оборотов диска. 2. Положите тело на покоящийся диск и включите проигрыватель. 3. Проделайте это несколько раз, изменяя радиус вращения тела R. Найдите минимальное значение радиуса окружности, при котором начинается скольжение тела по диску. 4. Результаты измерений и расчетов занесите в таблицу.
5. Оцените границы погрешности измерения коэффициента трения скольжения.
Границу относительной погрешности коэффициента трения можно вычислить по формуле:
ε μ= ε R+2 ε t+ ε g, но погрешностью ε g можно пренебречь, если считать g=9,8 м/с2. Следовательно Граница абсолютной погрешности измерения коэффициента трения равна
6. Запишите результат в виде
Контрольные вопросы. (§§25,37 Учебник Г.Я. Мякишев)
1. Сформулируйте второй закон Ньютона. Справедлив ли этот закон для произвольного тела или только для материальной точки? 2.Какие условия необходимы для того, чтобы тело двигалось с постоянным ускорением? 3.Дайте определение массы. 4.Когда возникает сила трения покоя? От чего зависят ее модуль и направление? В каких пределах может изменяться сила трения покоя? 5.Может ли сила трения скольжения увеличить скорость тела? 6. Какая сила сообщает ускорение автомобилю? 7. От чего зависит коэффициент трения скольжения?
Лабораторная работа№5 по теме:
ИЗМЕРЕНИЕ МАССЫ ТЕЛА МЕТОДОМ ГИДРОСТАТИЧЕСКОГО ВЗВЕШИВАНИЯ Повторить § 34, 35 «Фнзика-10» Г.Я.Мякишев Оборудование: динамометр школьный с заклеенной шкалой; измерительный цилиндр; тело неизвестной массы; штатив; сосуд с водой; линейка измерительная. Задание: Отградуируйте пружину и измерьте массу тела с помощью полученных пружинных весов. Метод выполнения работы Трудность работы заключается в том, что для градуировки пружины (определения ее жесткости) нет грузов известной массы. Эту трудность можно преодолеть, измерив удлинение x1 пружины при подвешивании к ней груза неизвестной массы т в воздухе, а затем удлинение x2 этой же пружины при погружении груза в воду. Запишем уравнение, равновесия груза на пружине в воздухе: mg = kx1 (1) (k — жесткость пружины) и уравнение равновесия этого же груза, опущенного в сосуд с водой: mg – FA=kx2, (2) где FA — архимедова сила, действующая на груз. Она равна FA = ρ0Vg, (3) где ρ 0 — плотность воды, V — объем тела. Измерив объем тела с помощью измерительного цилиндра, можно из выражений (1), (2) и (3) рассчитать жесткость пружины:
и искомую массу груза:
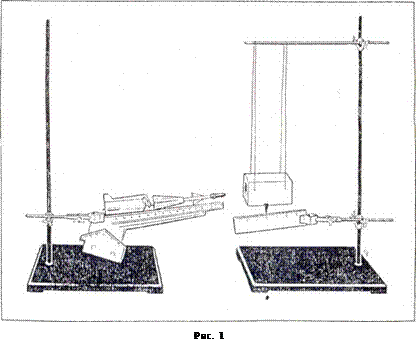
Порядок выполнения работы: 1. Укрепите динамометр с заклеенной шкалой в штативе. Проведите линию, фиксирующую положение конца ненагруженной пружины. 2. Подвесьте к пружине груз неизвестной массы и отметьте положение конца пружины. Измерьте линейкой удлинение x1 пружины. 3. Опустите груз в сосуд с водой (рис. 1) и измерьте новое удлинение х2 пружины. 4. Налейте в измерительный цилиндр определенный объем воды. Опустите в цилиндр груз и измерьте увеличение объема воды в измерительном цилиндре, равное объему V груза. 5. Вычислите жесткость k пружины по формуле (4) и массу груза по формуле (5).
В качестве границы абсолютной погрешности измерения объема 7. Результаты измерений и расчетов занесите в отчетную таблицу.
Отчетная таблица
Контрольные вопросы 1. Как можно измерить жесткость пружины, используя груз неизвестной массы? 2. Каким образом можно уменьшить погрешности измерений при выполнении работы описанным методом? 3. Сформулируйте закон Гука. При каких условиях он выполняется? 4. Сформулируйте закон Архимеда.
Лабораторная работа №6 по теме: ОПРЕДЕЛЕНИЕ СКОРОСТИ СНАРЯДА С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО МАЯТНИКА Повторить § 40, 50 «Фнзика-10». Г.Я. Мякишев В настоящей работе требуется определить методом баллистического маятника скорость снаряда, выпущенного «ракетной установкой». Для этого собирают установку, показанную на рисунке 1. С помощью лапки штатива «ракетную установку» укрепляют в горизонтальном положении точно против отверстия в коробке, подвешенной на длинных нитях, как маятник. Снаряд перед проведением опыта надевают на стержень со спиральной пружиной. При этом пружина сжимается и снаряд закрепляется специальным захватом. Затем производят выстрел. Снаряд застревает в коробке, сообщая ей импульс.
По закону сохранения импульса можно записать:
mv = (M+m)u,
где m — масса снаряда; v — его скорость; М — масса коробки; и — скорость коробки с застрявшим в ней снарядом. Если массы снаряда и коробки известны (их измеряют путем взвешивания), то для определения скорости снаряда v необходимо знать скорость и движения коробки после попадания в нее снаряда:
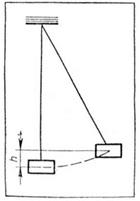
Применяя закон сохранения энергии, можно скорость коробки выразить через максимальную высоту ее подъема h по отношению к начальному уровню (рис. 2):
откуда
Высоту подъема h можно определить, измерив длину подвеса l и хорду АВ (рис. 3): BD2 = BC2 – CD2= l 2 – (l – h)2 = 2 lh – h 2, BD2 = AB2 – AD2 = s 2 – h 2, следовательно, 2 lh – h 2 = s 2 – h 2 или
Рис. 2 Рис. 3
Выполнение работы: Оборудование: 1) баллистический маятник (коробка, подвешенная на штативе); 2) игрушка «ракетная установка»; 3) штатив лабораторный; 4) измерительная линейка; 5) измерительная лента; 6) весы с разновесом.
1. Подготовьте в тетради таблицу для записи результатов измерений и вычислений.
2. С помощью весов определите массы снаряда и коробки (т, М), а измерительной лентой – длину нити подвеса l. 3. Произведите 3—5 выстрелов, измеряя каждый раз величину отклонения баллистического маятника s. Определите среднее значение отклонения scp. 4. Вычислите высоту h подъема маятника, скорость u и скорость снаряда v. 5. Полученные результаты внесите в таблицу. 6. Рассчитайте абсолютную и относительную погрешность измерений скорости снаряда.
Контрольные вопросы: 1. Поясните принцип действия данной установки по определению скорости снаряда. 2.Почему для нахождения скорости снаряда баллистического маятника не используется следующий способ вычислений:
3.Сформулируйте закон сохранения импульса. В каких случаях его можно применять? 4. Что называется полной механической энергией системы? Может ли сохраняться механическая энергия системы, на которую действуют внешние силы?
|


 . Эту формулу можно привести к виду:
. Эту формулу можно привести к виду:  . Где n- число оборотов, t – время, за которое диск сделал n оборотов, R – радиус окружности.
. Где n- число оборотов, t – время, за которое диск сделал n оборотов, R – радиус окружности.
 . Учитывая, что по оси ОY тело покоится, согласно первому закону Ньютона реакция опоры N равна по модулю силе тяжести mg, имеем
. Учитывая, что по оси ОY тело покоится, согласно первому закону Ньютона реакция опоры N равна по модулю силе тяжести mg, имеем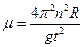
 .
.

 (4)
(4)

 (5)
(5) можно принять цену деления измерительного цилиндра, для границ абсолютных погрешностей измерения удлинений
можно принять цену деления измерительного цилиндра, для границ абсолютных погрешностей измерения удлинений  и
и 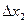 – цену деления измерительной линейки.
– цену деления измерительной линейки.






 ,
,  ?
?


