Абсолютный прирост
Выровненное значение определяется по формуле: уt=у0+A·t, где t - порядковый номер периода времени, начиная с «0» (0,1,2,3...), уt – теоретическое значение изучаемого явления, у0 -начальное значение ряда динамики.
Если А>0, значит наблюдается тенденция к увеличению и наоборот. Продление в будущее тенденции, наблюдающейся в прошлом, носит название экстраполяции (нахождение признака за пределами анализируемого периода). Нахождение по имеющимся данным за определенный период времени некоторых недостающих значений признака внутри этого периода называется интерполяцией. Метод аналитического выравнивания
Аналитическое выравнивание представляет собой наиболее точный способ выявления общей закономерности развития явления. При этом способе средняя линия развития, характеризующая общую закономерность, определяется путем построения соответствующих аналитических уравнений: прямой, параболы, гиперболы и т.д. Наиболее часто используемые виды функции в аналитическом выравнивании: -линейная y=a+Bt,где а - уровень ряда за период (в момент) времени t=0, в - средний абсолютный прирост уровня ряда за единичный промежуток времени; - показательная у=а+вt, где в - средний коэффициент роста за единичный промежуток времени; - параболическая y=a+bt+ct2,где с - квадратический параметр, равный половине ускорения, t - время, т.е. порядковые номера периодов или моментов времени. - гиперболическая y=a+ Расчет параметров при аналитическом выравнивании чаще всего производится с помощью метода наименьших квадратов, для этого чтобы найти неизвестные параметры уравнения а и в, решают систему уравнений:
где у - фактические уровни ряда n - число лет. Для упрощения расчетов в рядах динамики величинам t придают значения, которые при суммировании равны 0. При нечетном числе уровней ряда динамики для получения Σt = 0, уровень, находящийся в середине ряда, принимается за условное начало отсчета времени (значению соответствующему уровню присваивается ноль). Значения переменной времени расположенные левее этого уровня обозначаются натуральными числами со знаком (-) -1,-2,-3 и т. д., а расположенные правее этого уровня со знаком (+) +1,+2,+3 и т. д. Пример: У У У У У -2 -1 0 +1 +2 Если динамический ряд содержит четное количество членов, то обозначение следующее: У У У У У У -3 -2 -1 +1 +2 +3 Поскольку Σt = 0, то система уравнения имеет вид:
Рассмотрим пример аналитического выравнивания. Таблица 7 - Аналитическое выравнивание ряда динамики урожайности зерновых
a=17,8; b=-0,1; yt=17,8-0,1t - модель тренда y1=17,8-0,1(-2)=17,8+0,2=18,0 у2=17,8-0,1(-1)=17,8+0,1=17,9 у3=17,8-0,1(0)=17,8 и т.д. Экстраполируя при t=4 находим уровень урожайности 2016 года Прогнозный уровень у2016 = 17,8-0,1*4=17,4 + S, где S стандартная ошибка аппроксимации (среднее квадратическое отклонение) Где у и уt - фактические и расчетные значения уровней динамического ряда, n - число уровней ряда, 1- число параметров в уравнении тренда (а и в) l = 2. Таким образом, при условии сохранения тенденции к снижению (в < 0), урожайность зерновых в 2016 году составит 17,4 ц/га± S. Таким образом,аналитическое сглаживание позволяет не только определять общую тенденцию изменения явления на рассматриваемом отрезке времени, но и выполнять расчеты для таких периодов, в отношении которых нет исходных данных. ВЫБОР ВИДА ФУНКЦИИ ПРИ АНАЛИТИЧЕСКОМ ВЫРАВНИВАНИИ
Если относительно стабильны абсолютные приросты (первые разности уровней приблизительно равны) сглаживание можно проводить по прямой. 1. Если абсолютные приросты равномерно увеличиваются (вторые разности уровней приблизительно равны) можно применять параболу второго порядка. 2. При ускоренно возрастающих (замедляющих) абсолютных приростах применяют параболу третьего порядка. 3. При относительно стабильных темпах роста применяют показательную функцию. На практике выбор формы кривой может быть основан на анализе графического изображения уровней динамического ряда (линейная диаграмма). Целесообразней использовать графическое изображение сглаженных уровней, в которых случайные волны и колебания в некоторой степени оказываются погашенными. Например: для определения функции используют графическое изображение уровней динамического ряда.
Вопрос 4. Статистическое изучение сезонных колебаний При анализе рядов динамики важное значение имеет выявление сезонных колебаний. Этим колебаниям свойственны более или менее устойчивые изменения уровней ряда по внутригодовым периодам. Для измерения сезонных колебаний статистикой предложены следующие методы: а) метод абсолютных разностей; б) метод относительных разностей; в) построение индексов сезонности. Наличие сезонных колебаний выявляют с помощью графического метода. В этом случае применяют линейные диаграммы, на которые наносят данные об объеме явления по месяцам не менее чем за три года. а) Применяя способ абсолютных разностей определяют для каждого сезона (месяца, квартала, декады,) среднюю разность между фактическим (y) и выровненным (
у - фактические уровни ряда, m - число лет. б) При использовании метода относительных разностей определяют отношение абсолютных размеров указанных разностей к выровненному уровню:
При выявлении основной тенденции используют либо метод скользящей средней, либо аналитическое выравнивание. в) Индекс сезонности может быть рассчитан разными способам: - Если годовой уровень явления из года, в год остается относительно неизменным, то индексы сезонности исчисляются по формуле:
где (находится по формуле средней арифметической простой);
-Если уровни сезонного явления имеют тенденции к развитию (от года к году повышаются или снижаются), то индексы сезонности исчисляются по формуле:
где
Для сопоставления величины сезонных колебаний по нескольким предприятиям или периодам используют среднее квадратическое отклонение:
Чем меньше квадратическое отклонение, тем меньше величина сезонных колебаний. Контрольные вопросы по теме 6
Тема 7. Статистическое изучение взаимосвязи социально-экономических явлений Вопрос 1. Основные теоретические положения корреляционно- регрессионного анализа: причинность, регрессия, корреляция.
В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявить факторы (признаки), оказывающие существенное влияние на вариацию изучаемых явлений и процессов. Причинно-следственные отношения – это связь явлений и процессов, когда изменение одного из них – причины – ведет к изменению другого – следствие. Причина – это совокупность условий, обстоятельств, действие которых приводит к появлению следствия. Социально-экономические явления представляют собой результат одновременного воздействия большого числа причин. При изучении этих явлений необходимо выявить главные причины, абстрагируясь от второстепенных. В основе первого этапа статистического изучения связи лежит качественный анализ изучаемого явления, связанный с анализом природы социально или экономического явления, связанный с анализом природы социально и экономического явления методами экономической теории, социологии, конкретной экономики. Второй этап – построение модели связи. Он базируются на методах статистики: группировках, средних величинах, таблицах и т.д. Третий, последний этап – интерпретация результатов – вновь связан с качественными особенностями изучаемого признака. Статистика разработала множество методов изучения связей, выбор которых зависит от целей исследования и от поставленных задач. Признаки, обуславливающие изменение других, связанных с ними признаков, называются факторными. Признаки, изменяющиеся под действием факторных признаков, являются результативными. Связи между явлениями и их признаками классифицируются по степени тесноты связи, направлению и аналитическому выражению. В статистике различают функциональную и стохастическую зависимость. Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака. Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической связи является корреляционная связь,при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков. По степени тесноты связи различают количественные критерии оценки тесноты связи.
Таблица 12 - Количественные критерии оценки тесноты связи
По направлению выделяют связь прямую и обратную. При прямой связи с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. В случае обратной связи значение результативного признака изменяются под действием факторного, но в противоположном направлении по сравнению с изменением факторного признака. По аналитическому выражению выделяют связи: прямолинейные (или просто линейные),когда связь между явлениями может быть приближенно выражена уравнением прямой линии; нелинейные или криволинейные,если она выражается уравнением какой-либо кривой линии (параболы, гиперболы, степенной, показательной и т.д.). Для выявления наличия связи, ее характера и направления в статистике используются методы: проведение параллельных данных: аналитических группировок; графический; корреляции. Метод проведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере. С увеличением величины «х» величина «у» тоже возрастет, поэтому связь между ними прямая, и описать ее можно уравнением прямой или уравнением параболы второго порядка.
Графически взаимосвязь двух признаков изображается с помощью поля корреляции.
• • • • • • • • • • • • • • •
0 Х В системе координат на оси абсцисс откладывают значения факторного признака, а на оси ординат результативного. При отсутствии тесных связей имеет место беспорядочное расположение точек на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи. Для социально-экономических явлений характерно, что наряду с существенными факторами, формирующими уровень результативного признака на него оказывают воздействие многие другие неучтенные и случайные факторы. Это свидетельствует о том, что взаимосвязи явлений, которые изучает статистика, носят корреляционный характер и аналитически выражаются функцией вида Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой. В статистике принято различать следующие варианты зависимостей. 1. Парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными). 2. Частная корреляция – зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков. 3. Множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование. Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной) и между результативным и множеством факторных признаков (при многофакторной связи). Теснота связи количественно выражается величиной коэффициентов корреляции. Корреляция и регрессия тесно связаны между собой: первая оценивает силу (тесноту) статистической связи, вторая исследует ее форму. Та и другая служат для установления соотношения между явлениями, для определения наличия или отсутствие связи. Корреляционно- регрессионный анализ как общее понятия включает в себя измерения тесноты, направление связи и установления аналитического выражения (формы) связи (регрессионный анализ). Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (называемой зависимой или результативным признаком) обусловлено влиянием одной или нескольких независимых величин (факторов), а множество всех прочих факторов. А также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения. Регрессия может быть однофакторной (парной) и многофакторной (множественной). По форме зависимости различают: а) линейную регрессию,которая выражается уравнением прямой (линейной функцией) вида:
б) нелинейную регрессию,которая выражается уравнениями вида: парабола - гипербола -
По направлению связи различают: а) прямую регрессию (положительную), возникшую при условии, если с увеличением или уменьшением независимой величины, значения зависимой также соответственно увеличиваются или уменьшаются; б) обратную (отрицательную) регрессию, появляющуюся при условии, что с увеличением или уменьшением независимой величины, зависимая соответственно уменьшается или увеличивается.
|

 =1
=1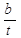

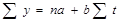 (для линейной зависимости)
(для линейной зависимости)

 ; а=
; а=  ; b=
; b= 

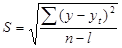
 ) уровнями:
) уровнями: , где
, где - сезонные изменения, i - номер сезона,
- сезонные изменения, i - номер сезона,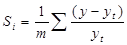 .
. ,
, - средняя из фактических уровней одноименных месяцев;
- средняя из фактических уровней одноименных месяцев; - общая средняя за исследуемый период.
- общая средняя за исследуемый период. ,
, - средняя из сглаженных (выровненных) уровней одноименных месяцев.
- средняя из сглаженных (выровненных) уровней одноименных месяцев. , где
, где - индекс сезонности, n – число месяцев (12).
- индекс сезонности, n – число месяцев (12).



 У
У • •
• • .
.

 и т.д.
и т.д.


