Графическое изображение положительной и отрицательной регрессии
• • • • • • •• •• • • • • • • • • • • • •• • •• • • • • • • •• • •• •
а) Прямая (положительная) регрессия б) Обратная (отрицательная) регрессия
Вопрос 2. Система показателей взаимосвязи, их вычисление и анализ
При наличии прямолинейной зависимости, определения тесноты связи производится с помощью коэффициента корреляции. Коэффициент корреляции представляет собой величину, которая изменяется в пределах от 0
Коэффициент детерминации, В тех случаях, когда связь между признаками
Прямолинейную зависимость можно выразить уравнением прямой
В уравнении прямолинейной корреляционной связи неизвестные параметры В основе этого способа лежит следующее требование: сумма квадратов отклонений фактических значений результативного признака (
Определение значений параметров
где – объем исследуемой совокупности (число единиц наблюдений)
Значения подставляют в уравнение, находят коэффициенты Полученные значения коэффициентов Параметр С целью расширения возможностей экономического анализа, для срав-нения роли различных факторов в формировании моделируемого показателя определяется коэффициент эластичности (Э) или Частный коэффициент эластичности показывает, на сколько процентов в среднем изменяется результативный признак (у) при изменении факторного (х) на 1%.
Определение регрессии при нелинейных корреляционных связях производится путем построения и решения уравнений, соответствующих различным типам кривых. Определить тип уравнения можно графически или если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, то связь между ними линейная, а при обратной связи – гиперболическая; если факторный признак увеличивается в арифметической прогрессии, а результативный – значительно быстрее, то используется параболическая или степенная регрессия. В тех случаях, когда установлена криволинейная зависимость, принимающая формулу параболы второго порядка, связь выражается уравнением кривой
Параметры
Оценка обратной зависимости между (х) и (у), когда с увеличением (уменьшением) (х) уменьшается (увеличивается) значение результативного признака (у), может быть осуществлена на основе уравнения гиперболы
Значимость линейного коэффициента корреляции проверяется на основе t- критерия Стьюдента.
k=n-2 – число факторных признаков, n – объем совокупности. Данный критерий оценки значимости применяется для совокупности n<50. Если расчетное значение При большем числе наблюдений (n>100) используется следующая формула
Вопрос 3. Методика проведения корреляционно-регрессионного анализа в рядах динамики При корреляционно-регрессионном анализе ряда динамики данные берутся минимум за 7 лет. 1) Строится таблица
Таблица 13- Вспомогательная таблица для расчета коэффициента корреляции
|


 •• •
•• • 0 Х 0
0 Х 0 1. Когда коэффициент корреляции равен «0» - связь линейная отсутствует, если он равен единице (с любым знаком), то между признаками существует функциональная связь. Знак
1. Когда коэффициент корреляции равен «0» - связь линейная отсутствует, если он равен единице (с любым знаком), то между признаками существует функциональная связь. Знак  Коэффициент корреляции может быть рассчитан по формуле:
Коэффициент корреляции может быть рассчитан по формуле: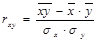 , где
, где - средняя величина из по парных произведений;
- средняя величина из по парных произведений; - средняя величина признака
- средняя величина признака  ;
; - средняя величина признака
- средняя величина признака  ;
;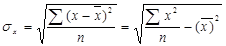 - среднее квадратическое отклонение по признаку
- среднее квадратическое отклонение по признаку  среднее квадратическое отклонение по признаку
среднее квадратическое отклонение по признаку  выраженный в %, показывает, сколько колебаний результативного признака обусловлено влиянием факторного.
выраженный в %, показывает, сколько колебаний результативного признака обусловлено влиянием факторного. (ню).
(ню). , где
, где - межгрупповая дисперсия результативного признака, вызванная влиянием признака-фактора;
- межгрупповая дисперсия результативного признака, вызванная влиянием признака-фактора;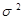 - общая дисперсия результативного признака;
- общая дисперсия результативного признака; - среднее значение результативного признака в соответствующих группах выделенных по величине признака-фактора;
- среднее значение результативного признака в соответствующих группах выделенных по величине признака-фактора; - общая средняя для всей совокупности.
- общая средняя для всей совокупности. , где
, где - среднее значение результативного признака;
- среднее значение результативного признака; - параметры уравнения;
- параметры уравнения;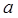 - значения
- значения 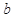 - коэффициент пропорциональности (регрессии).
- коэффициент пропорциональности (регрессии).


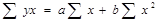
 - сумма значений факторного признака,
- сумма значений факторного признака,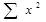 - сумма квадратов факторного признака,
- сумма квадратов факторного признака, - сумма значений результативного признака,
- сумма значений результативного признака, - сумма произведений значений факторного признака и значений результативного признака.
- сумма произведений значений факторного признака и значений результативного признака. - коэффициент.
- коэффициент. ; где b- коэффициент регрессии;
; где b- коэффициент регрессии; .
.
 находятся путем решения системы нормальных уравнений
находятся путем решения системы нормальных уравнений


 и системы нормальных уравнений
и системы нормальных уравнений

 с выходными параметрами (
с выходными параметрами (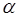 , k,
, k,  ),
), это свидетельствует о значимости линейного коэффициента корреляции и о статистической существенности зависимости между Х и У.
это свидетельствует о значимости линейного коэффициента корреляции и о статистической существенности зависимости между Х и У. .
.