Механика.
1.1. Скорость укорочения мышцы описывается уравнением 1.2. Движение летчика при катапультировании из реактивного самолета приближенно можно описать формулой 1.3. Уравнение вращательного движения твердого тела имеет вид: 1.4. Угловая скорость вращающегося тела изменяется по закону 1.5. Центрифуга, используемая для изучения влияния ускорения на организм человека, совершала 12 об/мин. Затем в течение 5 с число оборотов центрифуги изменилось так, что летчик стал испытывать ускорение 10 g. Определить угловое ускорение движения летчика, если он находился на расстоянии 7 м от оси вращения центрифуги. 1.6. Частота вращения медицинской центрифуги за 10 с изменилась с 1000 до 2500 об/мин. Определить угловое и максимальное центростремительное ускорения на расстоянии 10 см от оси вращения? 1.7. Фреза бормашины вращается с угловой скоростью ω. После выключения бормашины фреза, вращаясь равнозамедленно, сделала п оборотов. Определить время от момента выключения до остановки фрезы. 1.8. В ультрацентрифугах скорость смещения молекул исследуемого полимера в направлении от оси вращения выражается формулой 1.9. Диск массой т = 5 кг и радиусом R = 0,4 м вращается, делая п = 180 об/мин. Через t = 20 с после начала торможения диск останавливается. Найти момент сил торможения. 1.10. Фигурист вращается, делая n 1 = 6 об/с. Как изменится момент инерции фигуриста, если он прижмет руки к груди, и при этом частота вращения станет n 2 = 18 об/с? 1.11. Вентилятор начинает вращаться с постоянным угловым ускорением ε = 0,3 рад/с2 и через t 1 = 15 с после начала вращения приобретает момент импульса L 1 = 30 1.12. Ротор центрифуги массой 5 кг и радиусом 20 см был раскручен до 900 об/мин. После выключения электродвигателя под влиянием трения ротор остановился через 50 с. Найти момент силы трения, считая его постоянным, если ротор имеет вид диска. 1.13. Определить изменение угловой скорости вращения фигуриста при переходе в стойку «смирно», если в стойке «арабеск» скорость вращения составила 2 рад/с. Рассчитать работу, выполненную фигуристом при переходе из одной стойки в другую, считая момент инерции в стойке «арабеск» равным 8 кг · м2, в стойке «смирно» – 1,2 кг · м2. 1.14. Определить максимальную кинетическую энергию вращательного движения гимнаста массой 70 кг, выполняющего на перекладине «большие обороты», если в момент прохождения над перекладиной (стойка на руках) его скорость равнялась нулю. Момент инерции тела гимнаста относительно оси, проходящей через его общий центр тяжести (ОЦТ), равен 17 кг · м2, а расстояние от ОЦТ до перекладины 100 см. 1.15. Определить момент инерции рычага второго рода в системе для записи величины сокращения мышцы, если он представляет однородный алюминиевый стержень длиной 150 и диаметром 2 мм. 1.16. При нагрузке 100 Н скорость изотонического сокращения мышцы (сокращение при постоянной нагрузке) оказалась равной 2,2 см/с. Определить энергию, выделяющуюся в виде теплоты при сокращении мышцы. КПД мышцы 40 %, время сокращения 0,2 с. 1.17. При сокращении мышцы на х см затрачивается энергия 1.18. Назвать суставы тела человека, имеющие одну степень свободы. 1.19. Сколько степеней свободы допускают сочленения: тазобедренного сустава; плечевой и локтевой костей; лучевой и локтевой костей? 1.20. Сколько степеней свободы имеет предплечье относительно плеча? 1.21. Сколько степеней свободы имеют болт и гайка? Существует ли в теле человека сочленение такого типа? 1.22. Сколько степеней свободы имеет кисть руки относительно туловища, если плечо имеет три степени свободы относительно лопатки; плече-локтевое и локте-лучевое сочленения – две степени свободы; лучезапястное сочленение – также две степени свободы. 1.23. По законам механики шесть степеней свободы исчерпывают все возможные перемещения тела в пространстве. Какое значение имеет для человека наличие семи степеней свободы у кисти руки? 1.24. Каковы причины проигрыша в силе большинства рычагов, входящих в кинематические цепи тела человека? 1.25. В теле человека встречаются рычаги I и II рода. Имеются ли у него рычаги, которые используются как рычаги обоих родов? 1.26. Какая сила необходима для разрушения при сжатии бедренной кости диаметром 30 мм и толщиной стенок 3 мм, если предел прочности кости 1,4·108 Па? 1.27. Определить толщину стенки большой берцовой кости диаметром 28 мм, если ее разрыв произошел при нагрузке 23,1·103 Н. Предел прочности кости принять равным 9,8·107 Па. 1.28. Определить абсолютное удлинение сухожилия длиной 4 см и диаметром 6 мм под действием силы 31,4 Н. Модуль упругости сухожилия принять равным 109 Па. 1.29. При экспериментальном исследовании зависимости напряжения от удлинения для изолированной покоящейся мышцы было установлено, что при l / l 0 = 1,4 напряжение составило 7·105 Па. Определить модуль Юнга. 1.30. Мышца длиной 10 см и диаметром 1 см под действием груза 49 Н удлинилась на 7 мм. Определить модуль упругости мышечной ткани. 1.31. Определить силу, необходимую для удлинения сухожилия сечением 4 мм2 на 0,02 от его первоначальной длины. Модуль Юнга считать равным 109 Па. 1.32. Модуль упругости протоплазменных нитей, получившихся вытягиванием протоплазмы у некоторых типов клеток с помощью микроигл, оказывается равным 9·103 Па при комнатной температуре. Определить напряжение, действующее на нить при растяжениях, не превышающих 20 % ее первоначальной длины. 1.33. Нагрузка на бедренную кость, составляющая 1800 Н, при сжатии вызывает относительную деформацию, равную 5·10 -4. Определить эффективную площадь поперечного сечения кости, если модуль упругости ее равен 22,5·109 Па. 1.34. Какая работа совершается при растяжении на 1 мм мышцы длиной 5 см и диаметром 4 мм? Модуль Юнга для мышечной ткани принять равным 9,8·106 Па. 1.35. Найти потенциальную энергию, приходящуюся на единицу объема кости, если кость растянута так, что напряжение в ней составляет 3·109 Па. Модуль упругости кости принять равным 22,5·109 Па. 1.36. Вычислить работу, совершаемую спортсменом при растяжении пружины эспандера на 70 см, если известно, что при усилии в 10 Н эспандер растягивается на 1 см. 1.37. Написать уравнение гармонического колебания, если амплитуда ускорения am = 50 см/с2, частота колебания ν = 0,5 Гц, смещение точки от положения равновесия в начальный момент времени x 0 = 25 мм. Найти амплитуду скорости. 1.38. Написать уравнение гармонического колебания, если амплитуда скорости J m = 63 см/с, период колебаний Т = 1 с, смещение точки от положения равновесия в начальный момент времени равно нулю. Найти амплитуду ускорения, частоту колебаний. 1.39. Материальная точка массой т = 5 г колеблется согласно уравнению х = 10 cos (2 t + φ0), где х выражается в сантиметрах. Найти максимальную силу, действующую на точку, и полную энергию. 1.40. Уравнение колебаний материальной точки массой m = 16 г имеет вид: х = 2 sin (π t /8 + π/4), где х выражается в сантиметрах. Определить кинетическую, потенциальную и полную энергию точки через Δ t = 2 с после начала колебаний. 1.41. Барабан электрокимографа диаметром 16 см вращается с линейной скоростью 0,8 см/с. Пишущий элемент совершает колебания с частотой 1 Гц. Сколько полных колебаний будет записано на ленте за время одного оборота барабана? 1.42. Пишущий элемент регистрирующего прибора совершает колебания по закону х =2 sin π (t - 0,4) (см). Определить амплитуду, период и начальную фазу колебания. Через какое время после начала отсчета пишущий элемент будет проходить положение равновесия? 1.43. Камертон издает звук частотой 400 Гц. Определить максимальные скорость и ускорение конца ветви камертона, если амплитуда равна 0,2 мм. 1.44. Записать уравнение гармонического колебательного движения точки, если ее максимальное ускорение 158 см/с2, период колебаний 1 с и смещение точки от положения равновесия в начальный момент времени 2 см. 1.45. Тело массой 0,01 кг совершает гармонические колебания, уравнение которых имеет вид 1.46. Уравнение движения точки массой m имеет вид: 1.47. Чем объяснить, что при работе клепальным молотком 6-КМ, частота вибрации которого составляет 12 Гц, амплитуда, замеренная на локте, значительно превышает амплитуду вибрации самого инструмента (соответственно 1,16 и 0,33 мм)? Будет ли наблюдаться такое явление при частоте вдвое большей? 1.48. Насос для перекачки крови в аппарате «искусственное сердце» имеет диафрагму массой 10 г, совершающую затухающие колебания, описываемые уравнением 1.49. Два одинаково направленных колебания заданы уравнениями: 1.50. Два одинаково направленных гармонических колебания с одинаковой частотой и амплитудами А 1= 3 см и A 2 = 5 см складываются в одно гармоническое колебание с амплитудой А = 7 см. Найти разность фаз складываемых колебаний. 1.51. На вертикальный вход электронного осциллографа подаются напряжения U 1 = 4 cos 314 t и U 2 = 4 cos (314 t + α). Определить результирующее колебание. 1.52. Логарифмический декремент затухания камертона, колеблющегося с частотой ν = 100 Гц, равен λ = 0,002. Через, какой промежуток времени амплитуда колебаний камертона уменьшится в 100 раз? 1.53. Логарифмический декремент затухания маятника равен λ = 0,02. Во сколько раз уменьшится амплитуда после 50 полных колебаний? l.54. Амплитуда колебаний маятника уменьшается в 10 раз за 100 полных колебаний. Определить логарифмический декремент затухания. Через сколько колебаний амплитуда маятника уменьшилась в e раз? 1.55. Дифференциальное уравнение затухающих колебаний имеет вид: 1.56. Источник звука совершает колебания по закону: 1.57. Источник совершает колебания по закону: х = 5 sin 3140 t, где х выражается в метрах. Определить смещение от положения равновесия, скорость и ускорение точки, находящейся на расстоянии у = 340 м от источника, через Δ t = 1 с после начала колебания. Скорость распространения волны J = 340 м/с.
|

 , где x 0– полное укорочение мышцы; x – укорочение мышцы в данный момент; B – постоянная, зависящая от нагрузки. Записать закон сокращения мышцы x = x(t), если в момент времени t = 0 укорочение мышцы было равно нулю.
, где x 0– полное укорочение мышцы; x – укорочение мышцы в данный момент; B – постоянная, зависящая от нагрузки. Записать закон сокращения мышцы x = x(t), если в момент времени t = 0 укорочение мышцы было равно нулю. м. Определить скорость и ускорение летчика через 2 с после катапультирования.
м. Определить скорость и ускорение летчика через 2 с после катапультирования.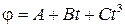 , где A = 2 рад, B = 3 рад/с, С = 1 рад/с3. Найти: 1) угол φ, угловую скорость ω и угловое ускорение ε в моменты времени: t 1 = 1 с, t 2 = 4 с; 2) среднюю угловую скорость ωср за промежуток времени Δt = t 2 – t 1.
, где A = 2 рад, B = 3 рад/с, С = 1 рад/с3. Найти: 1) угол φ, угловую скорость ω и угловое ускорение ε в моменты времени: t 1 = 1 с, t 2 = 4 с; 2) среднюю угловую скорость ωср за промежуток времени Δt = t 2 – t 1. , где A = 2 рад/с2, B = 3 рад/с3. На какой угол повернулось тело за время от t 1 = 1 с до t 2 = 3 с?
, где A = 2 рад/с2, B = 3 рад/с3. На какой угол повернулось тело за время от t 1 = 1 с до t 2 = 3 с? где b – постоянная величина; ω – угловая скорость центрифуги; х –расстояние от оси вращения до движущейся границы оседающего полимера. Определить уравнение движения границы полимера, если в момент времени t = 0 она находилась на расстоянии 0,5см от оси вращения.
где b – постоянная величина; ω – угловая скорость центрифуги; х –расстояние от оси вращения до движущейся границы оседающего полимера. Определить уравнение движения границы полимера, если в момент времени t = 0 она находилась на расстоянии 0,5см от оси вращения.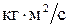 . Найти кинетическую энергию вентилятора через t 2= 20 с после начала вращения.
. Найти кинетическую энергию вентилятора через t 2= 20 с после начала вращения. , где A – теплота активации (постоянная величина); Рх –работа, совершаемая мышцей; ах –теплота укорочения (а –постоянная величина). Найти мощность, развиваемую мышцей при сокращении.
, где A – теплота активации (постоянная величина); Рх –работа, совершаемая мышцей; ах –теплота укорочения (а –постоянная величина). Найти мощность, развиваемую мышцей при сокращении. см. Найти значение, квазиупругой силы в момент времени t = 0,1 с.
см. Найти значение, квазиупругой силы в момент времени t = 0,1 с. . Найти зависимость кинетической и потенциальной энергии от времени.
. Найти зависимость кинетической и потенциальной энергии от времени. (см). Под действием внешней периодической силы ее колебания стали описываться уравнением
(см). Под действием внешней периодической силы ее колебания стали описываться уравнением  (см). Записать уравнение внешней периодической силы. Какова разность фаз между действующей силой и смещением?
(см). Записать уравнение внешней периодической силы. Какова разность фаз между действующей силой и смещением? ,
, 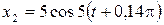 . Записать уравнение результирующего колебания.
. Записать уравнение результирующего колебания. . Определить коэффициент затухания и круговую частоту этих колебаний.
. Определить коэффициент затухания и круговую частоту этих колебаний. . Скорость распространения звука равна 340 м/с. Записать уравнение колебаний для точки, находящейся на расстоянии y = 102 м от источника. Потерями энергии пренебречь, волну считать плоской.
. Скорость распространения звука равна 340 м/с. Записать уравнение колебаний для точки, находящейся на расстоянии y = 102 м от источника. Потерями энергии пренебречь, волну считать плоской.


