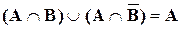Операции над множествами
Объединением множеств A и B (A È B) называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств, т.е A È B = { а ½ а Î A или а Î B }. Пересечением множеств A и B (A Ç B) называется множество, состоящее из всех элементов, принадлежащих каждому из этих множеств, т.е. А Ç B = { а ½ а Î А и а Î B }. Разностью множеств А и B (А \ B) называется множество, состоящее из всех элементов множества A, не принадлежащих множеству B, т.е. А \ B ={ а ½ а Î А и а Ï B }. Дополнением множества А в универсальном множестве U (
Симметрической разностью множеств A и B (обозначается A Å B или A D B = { а ½ либо а Î A и а Ï B, либо а Ï A и а Î B }, A D B = (A \ B) È (B \ A) = (A È B) \ (A Ç B). Операции над множествами можно проиллюстрировать графически с помощью кругов Эйлера (их также называют диаграммами Венна). В этом случае исходные множества изображают кругами или любыми другими замкнутыми линиями, а множество-результат выделяют штриховкой. Универсум обозначают прямоугольником.
Например: 1) Пусть множества
Тогда,
2) Пусть Тогда,
3)
Основные законы алгебры множеств: 1) Коммутативные законы
2) Ассоциативные законы
3)Дистрибутивные законы
4)Законы с Æ; и U А È Æ; = А А Ç U = А А È А Ç Æ; = Æ А È U = U А Ç
6) Законы идемпотентности
7) Законы поглощения А È (А Ç В) = А А È ( А Ç (А È В) = А А Ç ( 8) Законы де Моргана
9) Законы склеивания
|

 , ØА) называется множество, состоящее из всех элементов универсального множества U, не принадлежащих множеству А, т.е.
, ØА) называется множество, состоящее из всех элементов универсального множества U, не принадлежащих множеству А, т.е. .
. ) называется множество, состоящее из всех элементов, принадлежащих в точности одному из этих множеств, т.е.
) называется множество, состоящее из всех элементов, принадлежащих в точности одному из этих множеств, т.е.
 и
и  заданы на универсуме
заданы на универсуме 
 ,
, 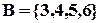 .
. ,
,  ,
,  ,
, ,
,  ,
, ,
,  .
. ,
,  .
.
 ,
, ,
, 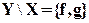 ,
,  ,
,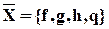 ,
,  .
. ,
,  ,
,  . Изобразить графически на диаграммах Эйлера множество
. Изобразить графически на диаграммах Эйлера множество  .
.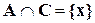 ,
,  , но
, но  , поэтому результат этой операции штриховкой отметить.
, поэтому результат этой операции штриховкой отметить.
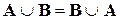





 = U
= U = Æ;
= Æ;  = U
= U ,
, 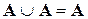 ,
,