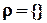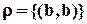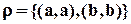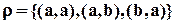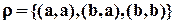Антисимметричность: .
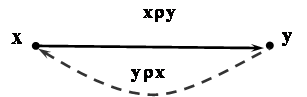
Отношение r на множестве X называется антисимметричным, если для всех Матрица антисимметричного отношения не имеет ни одной симметричной единицы относительно главной диагонали, а граф – для каждой дуги (x,y) не существует обратная дуга (y,x) и наоборот.
Свойства симметричности и антисимметричности не являются взаимоисключающими, примером может служить отношения равенства на множестве натуральных чисел. Например:
. На множестве людей: “быть выше”, ”быть равным”. На множестве множеств: Транзитивность:. Отношение
Например:
. На множестве людей: “быть выше”, ”обучаться в одной студенческой группе”. На множестве множеств: Отношение r на множестве X не является транзитивным, если существует, хотя бы один пример того, что для некоторых х,y,z множества Х из принадлежности (x,y) и (y,z) отношению r не следует, что (x,z) также принадлежит r. Например. 1) Отношение 2) Пусть задано двухэлементное множество Введем следующие обозначения: а) рефлексивность – Р; б) антирефлексивность – АР; в) симметричность – С; г) антисимметричность – АС; д) транзитивность – Т.
Отношение порядка – антисимметрично, транзитивно.
|
и 
из Х,из принадлежности (x,y) и (y,x) отношению r следует, что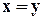 
.
,
,
,
,
, 
, 
.
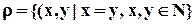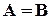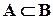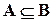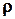на множестве 
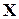называется транзитивным, если для всех 
измножества 
и 
отношению r следует, что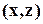 
также принадлежит r.
,
.
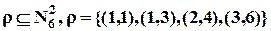и 
, не следует, что и пара 
принадлежит отношению 
определим все бинарные отношения на этом множестве: 
. Для всех отношений, заданных на множестве 
, определить наличие или отсутствие основных свойств.
