Отношение нестрого порядка ( ) – рефлексивно, антисимметрично, транзитивно.
Например:
. На множестве множеств: Отношение строгого порядка ( Например:
. На множестве множеств:“
Xпредшествуетyв смысле отношения нестрогого порядка”. Два элемента Если в упорядоченном множестве существует пара элементов x и y, для которой ни В отношениях полного порядка все элементы сравнимы между собой, а в отношениях частичного порядка не все элементы сравнимы между собой. Например: Отношения полного порядка:
. Отношения частичного порядка:
на множестве множеств: Отношение эквивалентности (~) – рефлексивно, Класс эквивалентности для элемента Например:
. На множестве людей: “иметь одно имя”, ”обучаться в одной студенческой группе”. На множестве множеств: Отношение эквивалентности разбивает Элементы, принадлежащие одному классу, находятся между собой в отношении эквивалентности, элементы из разных классов в отношении эквивалентности между собой не находятся. Например: Отношение Область определения: Область значений: Отношение Классы эквивалентности:
Например: Отношение Это отношение называют отношением сравнения по модулю
Отрезок натурального ряда Отношение сравнения по модулю 3 на
Область определения и область значений: Отношение Отношение Классы эквивалентности: Пусть Обратным отношением
Обратное отношение получается путём перестановки значений в парах исходного отношения. Пусть Композиция отношений
Например. .
.
|

 ,
,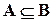 ,
, 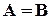 .
.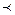 ) – антирефлексивно,
) – антирефлексивно, ,
,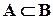 ”.
”.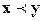 - “x предшествует y в смысле отношения строгого порядка”,
- “x предшествует y в смысле отношения строгого порядка”,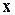 и
и  некоторого упорядоченного множества (множества, на котором существует отношение порядка) сравнимы между собой, если
некоторого упорядоченного множества (множества, на котором существует отношение порядка) сравнимы между собой, если 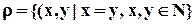 ,
,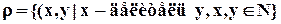 ,
,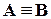 ,
, 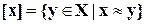 .
.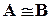 .
.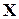 – множество, на котором задано отношение на непересекающиеся, которые называют классами эквивалентности.
– множество, на котором задано отношение на непересекающиеся, которые называют классами эквивалентности.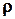 задано на множестве
задано на множестве 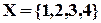 списком пар
списком пар  .
.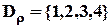 .
. .
.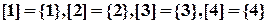 .
. .
.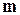 на множестве натуральных чисел.
на множестве натуральных чисел.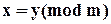 означает, что
означает, что 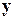 имеют одинаковый остаток при делении на
имеют одинаковый остаток при делении на 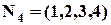 .
.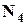 :
: .
.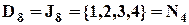 .
.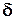 – рефлексивно, симметрично, транзитивно.
– рефлексивно, симметрично, транзитивно. .
. – некоторое бинарное отношение .
– некоторое бинарное отношение . называется отношение, которое определяется следующим образом:
называется отношение, которое определяется следующим образом: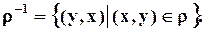
 – произвольные бинарные отношения такие, что
– произвольные бинарные отношения такие, что 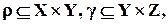 где
где 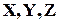 – некоторые множества.
– некоторые множества.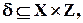 которое состоит из упорядоченных пар
которое состоит из упорядоченных пар  для которых существует такой элемент, что выполняются условия:
для которых существует такой элемент, что выполняются условия: 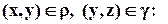
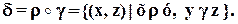
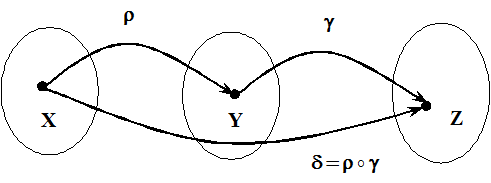
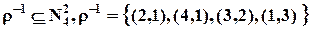 .
.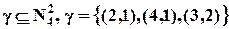 .
.



