Основные свойства проекций

При проецировании устанавливается геометрическая (проекционная) связь между оригиналом и его проекцией. Геометрические образы (формы) содержат в себе свойства, сохраняющиеся в проекциях при любых их преобразованиях. Рассмотрим основные свойства проекций.

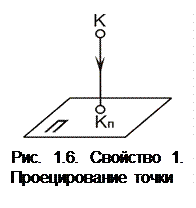
1. Проекция точки есть точка (рис. 1.6).

2. Проекция прямой линии на плоскость есть прямая линия (рис. 1.7, а), за исключением прямых линий, параллельных направлению проецирования, которые проецируются в точку (рис. 1.7, б).

а	б
Рис. 1.7. Свойство 2. Проецирование прямой линии: а – общий случай; б – частный случай

 

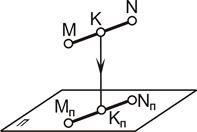
3. Проекция точки, принадлежащей прямой, есть точка, принадлежащая этой прямой (рис. 1.8).

Примечание. Свойства 1, 2, 3 являются общими для центрального и параллельного проецирования.

4. Точка пересечения проекций пересекающихся прямых линий является проекцией точки пересечения этих прямых линий (рис. 1.9).

Рис. 1.8. Свойство 3. Проецирование точки, принадлежащей прямой линии	Рис. 1.9. Свойство 4. Проецирование пересекающихся прямых линий

5. Проекции параллельных прямых линий параллельны и имеют одно направление, а длины их находятся в таком же соотношении, как и длины самих отрезков (рис. 1.10).

6. Проекция точки делит проекцию отрезка в том же отношении, в каком точка делит отрезок (рис. 1.11).

Рис. 1.10. Свойство 5. Проецирование параллельных прямых линий	Рис. 1.11. Свойство 6. Проецирование отношения отрезков прямой линии

 

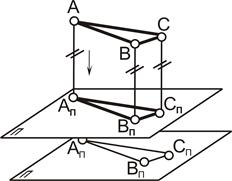
Примечание. Свойства 4, 5, 6 характерны только для параллельного проецирования.

7. Если прямая линия либо плоская фигура параллельна плоскости проекций, то она проецируется на эту плоскость в натуральную величину (рис. 1.12).

8. При параллельном переносе плоскости проекций величина проекций остается неизменной (рис. 1.13).

Рис. 1.12. Свойство 7. Проецирование плоской фигуры (треугольника)	Рис. 1.13. Свойство 8. Проецирование плоскости при параллельном переносе

 

9. Если одна сторона прямого угла параллельна плоскости проекций, то угол на эту плоскость проецируется в натуральную величину
(рис. 1.14).

Рис. 1.14. Свойство 9. Проецирование прямого угла

Доказательство. Дан прямой угол АВС, у которого по условию прямая
(ВС) (АВ) и (ВС) || П₁ плоскости проекций. По построению прямая (ВС) (ВВ₁) (проецирующему лучу). Следовательно, пря­мая ВС β (АВхВВ₁), так как она перпендикулярна к двум пересекающим­­ся прямым, лежащим в этой плоскости. По условию прямая (В₁С₁) || (ВС), поэтому (В₁С₁) β, т. е. и прямой (А₁В₁) этой плоскости. Следовательно, угол между прямыми (А₁В₁) и (В₁С₁) равен 90°, что и требовалось доказать.

Примечание. Свойства 7, 8, 9 справедливы для прямоугольного проецирования.