Положение точки относительно плоскостей проекций
Положение точки в пространстве относительно плоскостей проекций определяется её координатами. Координатой Х определяется удалённость точки от плоскости П3 (проекция на П2 или П1), координатой
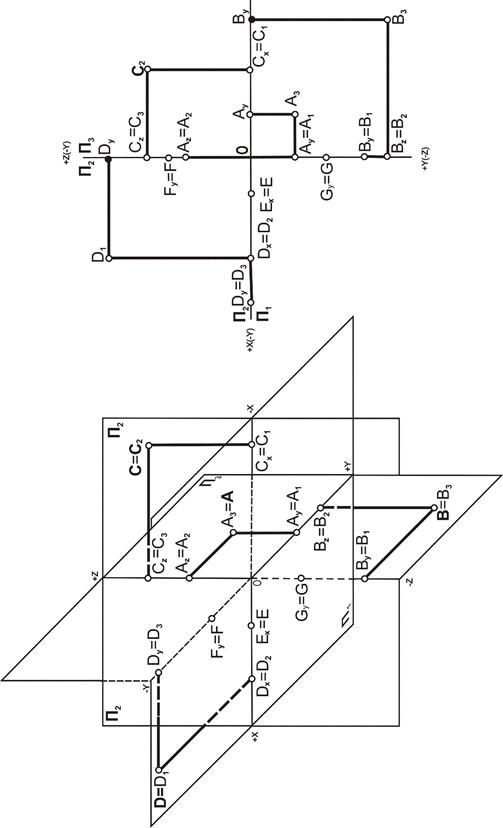
Рис. 3.1. Классификация точек Точка общего положения. Координаты точки общего положения не равны нулю (x≠0,y≠0,z≠0), и в зависимости от знака координаты точка может располагаться в одном из восьми октантов (табл. 2.1). На рис. 3.2 даны чертежи точек общего положения. Анализ их изображений позволяет сделать вывод, что они располагаются в следующих октантах пространства: А(+X;+Y; +Z (Ì;I октанту; B(+X;+Y;-Z(Ì;IV октанту; C(-X;+Y; +Z (Ì;V октанту; D(+X;+Y; +Z (Ì;II октанту. Точки частного положения. Одна из координат у точки частного положения равна нулю, поэтому проекция точки лежит на соответствующем поле проекций, другие две – на осях проекций. На рис. 3.3 такими точками являются точки А, В, C, D, G. A Ì;П3,то точка ХА=0; В Ì;П3,то точка ХВ=0; С Ì;П2,то точка YC=0; D Ì;П1,то точка ZD=0. Точка может принадлежать сразу двум плоскостям проекций, если она лежит на линии пересечения этих плоскостей – оси проекций. У таких точек не равна нулю только координата на этой оси. На рис. 3.3 такой точкой является точка G (G Ì;OZ,то точка ХG=0, YG=0).
|