Использование комплексных чисел для расчёта электрических цепей при синусоидально изменяющихся напряжениях, токах и ЭДС

Если принять модуль и аргумент комплексного числа равными амплитуде и фазе тока, напряжения и ЭДС, то получим комплексы мгновенных значений этих переменных.

 

i = I_m e^{j(ωt +Ψi)} ; u = U_me^{j(ω t + Ψu)} ; e = E_me^{j(ω t + Ψe).}

j

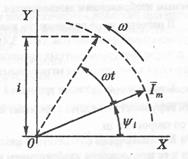
Обратите внимание на то, что при увеличении времени t вектор тока вращается против часовой стрелки с угловой частотой ω;. А проекция этого вектора на мнимую ось будет полностью соответствовать мгновенному значению тока.

i = I_m sin(ωt +Ψ_i)

 

Рис. 4.2. Вектор тока на

комплексной плоскости

Аналогично проекции векторов напряжения и ЭДС на мнимую ось будут соответствовать мгновенным значениям этих величин.

 

u = U_m sin(ωt +Ψ_u); e = E_m sin(ωt +Ψ_e).

То есть для расчёта электрических цепей при синусоидальных токах напряжениях и ЭДС можно использовать комплексные числа, математические операции с которыми выполняются достаточно просто. А для нахождения действительного (синусоидального) изменения рассчитанных с помощью комплексных чисел величин во времени необходимо взять мнимую часть результатов расчёта.

Для расчёта используются комплексы амплитудного значения.

 

Ψe

Ì_m = I_m e^jΨi ; Ù_m = U_me^jΨu ; È_m = E_me^{j Ψe} ,

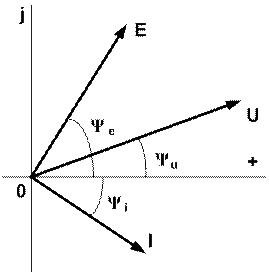
где Ì_m, Ù_m, È_m – комплексы амплитудного значения тока, напряжения и ЭДС,

I_m, U_m, E_m, Ψ_i, Ψ_u, Ψ_e – амплитудное значение тока, напряжения и ЭДС и их начальные фазы.

Однако чаще для расчёта цепей и построения диаграмм (рис. 5.3) используются комплексы действующего напряжения, тока и ЭДС.

Ψe

Ì = I e^jΨi ; Ù = Ue^jΨu ; È = Ee^{j Ψe} ,

где Ì, Ù, È – комплексы действующего значения тока, напряжения и ЭДС,

I, U, E, Ψ_i, Ψ_u, Ψ_e – действующие значения тока, напряжения и ЭДС и их начальные фазы.

Рис. 5.3. Векторы ЭДС, напряжения

и тока на комплексной плоскости