Теоретическая часть. На точечный заряд q, движущийся со скоростью в магнитном поле c индукцией , действует сила Лоренца
На точечный заряд q, движущийся со скоростью Суть эффекта Холла рассмотрим на следующем примере: Образец в виде прямоугольной пластинки полупроводника поместим в магнитное поле (рис.1,а), направленное от нас, и пропустим через образец электрический ток плотностью j слева направо.
а) б) Рис 1. Образец для измерения холловского напряжения
В полупроводнике носителями заряда являются отрицательно заряженные электроны и положительно заряженные дырки. Сила Лоренца, действующая на них, имеет одинаковое направление, не смотря на то, что электроны и дырки движутся в противоположных направлениях (объясните почему). Если концентрация носителей одного типа преобладает (примесный полупроводник n - или р- типа), то верхняя и нижняя грани пластинки будут заряжены зарядами противоположного знака. (Определите, какого типа полупроводник изображен на рис.1,а). При этом возникает противоположное по отношению к Если наряду с магнитным существует и электрическое поле, то сила Лоренца приобретает вид: . При отсутствии тока в поперечном направлении проекция силы Лоренца на это направление равна нулю: Ех = VB. (1) Это выражение будет использовано для определения разности потенциалов Холла. Рассмотрим некоторые вопросы о проводимости исследуемого материала (в настоящей работе этот материал - полупроводник p -типа). В полупроводнике ток может быть разделен на электронную и дырочную составляющие:
Здесь Движение носителей (дрейф) вызывается "продольным" полем
Коэффициент пропорциональности m называется подвижностью носителей. По закону Ома
и проводимость
В примесном полупроводнике одна из составляющих преобладает, поэтому в полупроводнике n- и p- типа проводимость равна
Различие в концентрациях носителей часто достигает нескольких порядков, тогда как отношение подвижностей не слишком велико (обычно Для определения проводимости материала может быть использован показанный на рис.1,б образец. Плотность тока через образец
продольное напряжение на образце
здесь S - площадь поперечного сечения, l, b и d – длина, ширина и толщина образца. Отсюда получаем для полупроводника р - типа
или Для измерения поперечной холловской разности потенциалов (холловского напряжения)
Холловское напряжение равно
где величина
называется постоянной Холла. Она зависит от концентрации носителей (в данном случае дырок), и поэтому, измеряя постоянную Холла, можно определить концентрацию носителей в полупроводнике.
|

 в магнитном поле c индукцией
в магнитном поле c индукцией 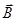 , действует сила Лоренца
, действует сила Лоренца  . Эта сила, перпендикулярная и скорости движения заряда, и направлению магнитного поля приводит к эффекту Холла, который можно наблюдать в металлах и полупроводниках.
. Эта сила, перпендикулярная и скорости движения заряда, и направлению магнитного поля приводит к эффекту Холла, который можно наблюдать в металлах и полупроводниках.

 электрическое поле
электрическое поле  (рис.1,б). Это поле называется полем Холла, а явление возникновения поперечного электрического поля под действием магнитного поля называется эффектом Холла.
(рис.1,б). Это поле называется полем Холла, а явление возникновения поперечного электрического поля под действием магнитного поля называется эффектом Холла. . В результате
. В результате .
. - элементарный заряд,
- элементарный заряд,  и
и  - концентрации электронов и дырок,
- концентрации электронов и дырок,  и
и  - средние скорости движения электронов и дырок.
- средние скорости движения электронов и дырок. . Скорость дрейфа пропорциональна напряженности поля:
. Скорость дрейфа пропорциональна напряженности поля: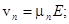
 .
. ,
, .
. или
или 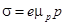 .
. ), так что эти равенства выполняются с большой точностью.
), так что эти равенства выполняются с большой точностью.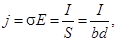

 ,
, . (2)
. (2) служат контакты а, a'. Если прибор для ее измерения имеет высокое входное сопротивление, то ток через контакты а, а' практически равен нулю. Поэтому справедливо выражение (1) и
служат контакты а, a'. Если прибор для ее измерения имеет высокое входное сопротивление, то ток через контакты а, а' практически равен нулю. Поэтому справедливо выражение (1) и .
.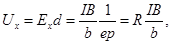 (3)
(3) (4)
(4)


