Понятие мультиколлинеарности факторов.

Мультиколлениарность факторов – тесная корреляционная взаимосвязь между отбираемыми для анализа факторами, совместно воздействующими на общий результат, которая затрудняет оценивание регрессионных параметров

– наличие высокой линейной связи между всеми или несколькими факторами.

Причинами возникновения мультиколлинеарности между признаками являются:

1. Изучаемые факторные признаки, характеризуют одну и ту же сторону явления или процесса. Например, показатели объема производимой продукции и среднегодовой стоимости основных фондов одновременно включать в модель не рекомендуется, так как они оба характеризуют размер предприятия;

2. Использование в качестве факторных признаков показателей, суммарное значение которых представляет собой постоянную величину;

3. Факторные признаки, являющиеся составными элементами друг друга;

4. Факторные признаки, по экономическому смыслу дублирующие друг друга.

5. Одним из индикаторов определения наличия мультиколлинеарности между признаками является превышение парным коэффициентом корреляции величины 0,8 (rxi xj) и др.

Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон, и в результате нельзя будет оценить воздействие каждого фактора в отдельности.

Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:

1) оценки параметров становятся ненадежными, обна­руживают большие стандартные ошибки и меняются с из­менением объема наблюдений (не только в величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

2) затрудняется интерпретация параметров множест­венной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированны; параметры линейной регрессии теряют экономический смысл;

3) нельзя определить изолированное влияние факторов на результативный показатель.

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлениарность факторов и ненадежнее результаты множественной регрессии. Чем ближе определитель к 1 – тем ниже мультиколлениарность.

Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.

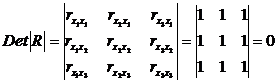
Существуют различные подходы преодоления сильной межфакторной корреляции. Простейший из них - исключе­ние из модели фактора (или факторов), в наибольшей сте­пени ответственных за мультиколлинеарность при условии, что качество модели при этом пострадает несущественно (а именно, снизится несущественно).